Hostname: page-component-586b7cd67f-tf8b9 Total loading time: 0 Render date: 2024-11-30T19:03:34.287Z Has data issue: false hasContentIssue false
  • English
  • Français

Modeles Bifiltres: Une Plaque Tournante en Homotopie Rationnelle

Published online by Cambridge University Press:  20 November 2018

Yves Felix
Yves Felix*
Affiliation:
Université Catholique de Louvain, Louvain–La-Neuve, Belgique
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

A chaque c.w. complexe X, 1-connexe, de type fini, est associé une algèbre différentielle graduée commutative (ΛZ, d) qui est un modèle dans le sens de Sullivan [10] et représente donc le type d'homotopie rationnelle de X.

ΛZ est munie d'une seconde graduation Z = ⊕q≧0Zq. La différentielle d se décompose alors sous la forme 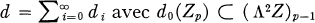et d0(Zp) ⊂ (Λ2Z)p–1 et di(Zp) ⊂ Zp–i, i ≧ 1. En particulier d0 est purement quadratique tandis que di est du premier degré, i ≧ 1.

L'algèbre ΛZ et la partie quadratique d0 ne dépendent que des nombres de Betti de X. Les différents types d'homotopie rationnelle de nombres de Betti donnés sont donc paramétrés par les déformations di. La partie d1 exprime la structure multiplicative de l'algèbre de cohomologie rationnelle de X, les parties d2, d3, d4. … les structures algébriques plus complexes du type d'homotopie rationnelle.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 33 , Issue 6 , 01 December 1981 , pp. 1448 - 1458
Copyright
Copyright © Canadian Mathematical Society 1981

References

1. Baues, H. J. et Lemaire, J. M., Minimal models in homotopy theory, Math. Ann 225 (1977), 219–242.Google Scholar
2. Cartan, H. et Eilenberg, S., Homologuai algebra (Princeton University, 1956).Google Scholar
3. Felix, Y., Dénombrement des types de k-homolopie—théorie de la déformation (a paraître Nouveaux Mémoires de la Soc. Math. France).Google Scholar
4. Halperin, S. et Stasheff, J. D., Obstructions to homotopy equivalence, Advances in Math. 32 (1979), 233–279.Google Scholar
5. Lehmann, D., Théorie homotopique des formes différentielles, Astérisque 45 (1977).Google Scholar
6. Lemaire, J. M. et Sigrist, F., Dénombrement des types d'homotopie rationelle, Comptes Rendus de l'Acad. Française (1978).Google Scholar
7. Neisendorfer, J., Lie algebras, coalgebras and rational homotopy theory of nilpotent spaces, Proc. J. of Math. 75 (1978), 429–460.Google Scholar
8. Quillen, D., Rational homotopy theory, Ann. of Math. 90 (1969), 205–295.Google Scholar
9. Schlessinger, M. et Stasheff, J. D., Deformation theory and rational homotopy type (preprint, 1979).Google Scholar
10. Sullivan, D., Infinitesimal computations in topology, Publ. de l'I.H.E.S. 47 (1978), 269–331.Google Scholar
11. Tanré, D., Modèles de Chen, Sullivan et Quillen (publication Irma 2, Lille, 1980).Google Scholar