Hostname: page-component-cd9895bd7-7cvxr Total loading time: 0 Render date: 2024-12-26T17:04:22.420Z Has data issue: false hasContentIssue false
  • English
  • Français

A Mixed Parseval's Equation And a Generalized Hankel Transformation of Distributions

Published online by Cambridge University Press:  20 November 2018

J. J. Betancor
J. J. Betancor*
Affiliation:
University of La Laguna, La Laguna, Canary Islands
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let an integral transform T﹛f﹜ of a complex valued function f(x) defined over the interval (0, ∞) be defined as 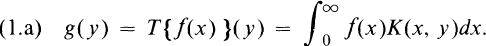One of the most usual procedures to extend the classical transform (l.a) to generalized functions consists in constructing a space A of testing functions over (0, ∞) which is closed with respect to the classical transform (l.a) and then the corresponding transform of the generalized function/ of the dual space of A is defined through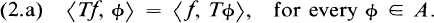

This approach has been followed by L. Schwartz [13] and A. H. Zemanian [20], amongst others.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 41 , Issue 2 , 01 April 1989 , pp. 274 - 284
Copyright
Copyright © Canadian Mathematical Society 1989

References

1. Altenburg, G., Bessel transformationen in Raumen von Grundfunktionen uber dem intervall fi = (0, ∞) und derem dual raumen, Math. Nachr. 108 (1982), 197–218.Google Scholar
2. Betancor, J.J., La transformation integral /Fa 0,a1, a 2, Doctoral Thesis, Depart. Math. Anal., Univ. of La Laguna, Tenerife, Spain (1987).Google Scholar
3. Dimovski, I., Operational calculus for a class of differential operators, Compt. Rend. L’Academie Bulgare Sci. 19 (1966), 1111–1114.Google Scholar
4. Gelfand, I.M. and Shilov, G.E., Generalized functions, I and 2 (Academic Press, New York, 1964, 1968).Google Scholar
5. Gray, A., Mathews, G.B. and McRobert, T.M., A treatise on Bessel functions and their applications to physics (McMillan and Co. Ltd., London, 1952).Google Scholar
6. Koh, E.L. and Zemanian, A.H., The complex Hankel and I-transformations of generalized functions. SIAM J. Appl. Math. 16 (1968), 945–957.Google Scholar
7. Lee, W.Y., On Schwartz's Hankel transformation of certain spaces of distributions, SIAM J. Math. Anal., 6 (2) (1975), 427–432.Google Scholar
8. McBride, A., The Hankel transformation of some classes of generalized functions and connections with fractional integration, Proc. Roy. Soc. Edinburgh 81 A (1978), 95–117.Google Scholar
9. Mendez, J.M., La transformation integral de Hankel-Clifford, Secretariado de Publicaciones de la Universidad de La Laguna, Coleccion Monografias, 8 (Tenerife, Spain, 1981).Google Scholar
10. Mendez, J.M., On the Bessel transform of arbitrary order, Math. Nachr. 136 (1988), 233–239.Google Scholar
11. Mendez, J.M., A mixed Parseval equation and the generalized Hankel transformation, Proc. Amer. Math. Soc. 102 (1988), 619–624.Google Scholar
12. Schuitman, A., On a certain test function space for the Schwartz's Hankel transformation, Delft Progr. Report 2 (1977), 193–206.Google Scholar
13. Schwartz, L., Théorie des distributions (Hermann, Paris, 1966).Google Scholar
14. Schwartz, A.L., An inversion theorem for Hankel transforms, Proc. Amer. Math. Soc. 22 (1969), 713–717.Google Scholar
15. Sneddon, I.N., The use of integral transforms (McGraw Hill Book Co., New York, 1972).Google Scholar
16. Socas, M.M., La transformation integral de Hankel-Clifford en tiertos espacios de funciones generalizadas, Doctoral Thesis, Depart. Math. Anal., Univ. of La Laguna, Tenerife, Spain, 1986.Google Scholar
17. Titchmarsh, E.C., Introduction to the theory of Fourier integrals (Oxford University Press, Oxford, 1948).Google Scholar
18. Watson, G.N., A treatise on the theory of Bessel functions (Cambridge University Press, Cambridge, 1958).Google Scholar
19. Zemanian, A.H., Distribution theory and transform analysis (McGraw Hill Book Co., New York, 1965).Google Scholar
20. Zemanian, A.H., A distributional Hankel transformation, J. SIAM Appl. Math. 14 (1966), 561–576.Google Scholar
21. Zemanian, A.H., Generalized integral transformation (Interscience Publishers, New York, 1968).Google Scholar