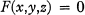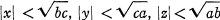Minimal Solutions of Diophantine Equations

L. Holzer

doi:10.4153/CJM-1950-021-0

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Our aim is to prove: If a, b, c are positive integers, if ab > 1, if a, b, c are relatively prime in pairs, and all are free of squares, if — ab is a quadratic residue of c, bc of a, ca of b, and if F(x, y, z) = ax2 + by2 — cz2, we have non-trivial solutions of

with the inequalities

Crossref Citations

This article has been cited by the following publications. This list is generated based on data provided by Crossref.

Mordell, L. J. 1951. On the equation ax2+by2?cz2=0. Monatshefte f�r Mathematik, Vol. 55, Issue. 4, p. 323.

Cassels, J. W. S. 1955. Bounds for the least solutions of homogeneous quadratic equations. Mathematical Proceedings of the Cambridge Philosophical Society, Vol. 51, Issue. 2, p. 262.

Von Kneser, Martin 1959. Kleine Lösungen der diophantischen Gleichungax 2 +by 2 =cz 2. Abhandlungen aus dem Mathematischen Seminar der Universität Hamburg, Vol. 23, Issue. 1, p. 163.

Mordell, L.J. 1969. On the magnitude of the integer solutions of the equation ax2 + by2 + cz2 = 0. Journal of Number Theory, Vol. 1, Issue. 1, p. 1.

1969. Vol. 30, Issue. , p. 42.

CrossRef

Siegel, Carl Ludwig Chandrasekharan, K. and Maaß, H. 1979. Gesammelte Abhandlungen. p. 250.

Lagarias, J. C. 1980. On the computational complexity of determining the solvability or unsolvability of the equation 𝑋²-𝐷𝑌²=-1. Transactions of the American Mathematical Society, Vol. 260, Issue. 2, p. 485.

Cochrane, Todd and Mitchell, Patrick 1998. Small Solutions of the Legendre Equation. Journal of Number Theory, Vol. 70, Issue. 1, p. 62.

Granville, A. 2010. Rational and Integral Points on Quadratic Twists of a Given Hyperelliptic Curve. International Mathematics Research Notices,

Narkiewicz, Władysław 2012. Rational Number Theory in the 20th Century. p. 131.

Leal-Ruperto, José Luis 2014. On the magnitude of the Gaussian integer solutions of the Legendre equation. Journal of Number Theory, Vol. 145, Issue. , p. 572.

Diaz-Vargas, Javier and Vargas de los Santos, Gustavo 2018. The Legendre equation in Euclidean imaginary quadratic number fields. Journal of Number Theory, Vol. 186, Issue. , p. 439.

Leal-Ruperto, José Luis 2019. On the magnitude of the integer solutions of the semi-diagonal equation ax2 + by2 + cz2 + dxy = 0. International Journal of Number Theory, Vol. 15, Issue. 01, p. 157.

Leal-Ruperto, José Luis and Leep, David B. 2019. Holzer’s theorem in k[t] . The Ramanujan Journal, Vol. 48, Issue. 2, p. 351.

Shaw, James D. Guyker, James and Solovjovs, Sergejs 2023. On Parametric and Matrix Solutions to the Diophantine Equation x2 + dy2 − z2 = 0 Where d Is a Positive Square‐Free Integer. International Journal of Mathematics and Mathematical Sciences, Vol. 2023, Issue. 1,

Skorobogatov, Alexei N. and Sofos, Efthymios 2023. Schinzel Hypothesis on average and rational points. Inventiones mathematicae, Vol. 231, Issue. 2, p. 673.

Grechuk, Bogdan 2024. Polynomial Diophantine Equations. p. 235.

Article contents

Minimal Solutions of Diophantine Equations

Extract

Save article to Kindle

Save article to Dropbox

Save article to Google Drive

Reply to: Submit a response

Your details

You have entered the maximum number of contributors

Conflicting interests