Article contents
Mercerian Conditions for the Method (F, dn)
Published online by Cambridge University Press: 20 November 2018
Extract
This paper sets forth conditions sufficient that the generalized Lototsky method (F, dn) be regular and Mercerian. If the dn's are real and of constant sign, then the conditions are also necessary. Moreover, it follows that if f is a polynomial, then under the same conditions the method (f,dn) is equivalent to the Sonnenschein method generated by f . Various related results are also given.
Definition 2.1. Let f be a nonconstant function holomorphic on the closed unit disk and let 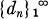 be a complex sequence with f (l) + dn ≠ 0. Suppose
be a complex sequence with f (l) + dn ≠ 0. Suppose
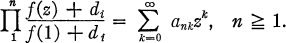
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 1971
References
- 1
- Cited by


