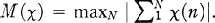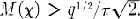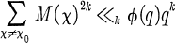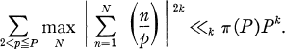Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Burgess, D. A.
1986.
Mean values of character sums.
Mathematika,
Vol. 33,
Issue. 1,
p.
1.
Baker, R. C.
and
Montgomery, Hugh L.
1990.
Analytic Number Theory.
Vol. 85,
Issue. ,
p.
23.
Murty, M. Ram
and
Murty, V. Kumar
1997.
Non-vanishing of L-Functions and Applications.
Vol. 157,
Issue. ,
p.
133.
Cochrane, Todd
and
Zheng, Zhiyong
1998.
High order moments of character sums.
Proceedings of the American Mathematical Society,
Vol. 126,
Issue. 4,
p.
951.
Rivat, J.
and
Sárközy, András
2006.
General Theory of Information Transfer and Combinatorics.
Vol. 4123,
Issue. ,
p.
343.
Garaev, M.Z.
and
Garcia, V.C.
2008.
The equation x1x2=x3x4+λ in fields of prime order and applications.
Journal of Number Theory,
Vol. 128,
Issue. 9,
p.
2520.
Xu, Zhefeng
2009.
MEAN VALUE OF THE CHARACTER SUMS OVER INTERVAL.
Taiwanese Journal of Mathematics,
Vol. 13,
Issue. 1,
Gallagher, P. X.
and
Montgomery, H. L.
2010.
A note on Burgess’s estimate.
Mathematical Notes,
Vol. 88,
Issue. 3-4,
p.
321.
Галлахер, П К
Gallagher, P X
Монтгомери, Х Л
and
Montgomery, H L
2010.
Об оценке Бeрджесса.
Математические заметки,
Vol. 88,
Issue. 3,
p.
355.
Cochrane, Todd
and
Shi, Sanying
2010.
The congruence x1x2≡x3x4(modm) and mean values of character sums.
Journal of Number Theory,
Vol. 130,
Issue. 3,
p.
767.
Pomerance, Carl
2011.
Remarks on the Pólya–Vinogradov Inequality.
Integers,
Vol. 11,
Issue. 4,
Bober, Jonathan W.
and
Goldmakher, Leo
2013.
THE DISTRIBUTION OF THE MAXIMUM OF CHARACTER SUMS.
Mathematika,
Vol. 59,
Issue. 2,
p.
427.
Kerr, Bryce
2017.
On the congruence x1x2≡x3x4modq.
Journal of Number Theory,
Vol. 180,
Issue. ,
p.
154.
Dartyge, Cécile
Gyarmati, Katalin
and
Sárközy, András
2018.
On Irregularities of Distribution of Binary Sequences Relative to Arithmetic Progressions, II (Constructive Bounds).
Uniform distribution theory,
Vol. 13,
Issue. 2,
p.
1.
BONOLIS, DANTE
2022.
On the size of the maximum of incomplete Kloosterman sums.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 172,
Issue. 3,
p.
563.
Lamzouri, Youness
2024.
The distribution of large quadratic character sums and applications.
Algebra & Number Theory,
Vol. 18,
Issue. 11,
p.
2091.
Szabó, Barnabás
2024.
High moments of theta functions and character sums.
Mathematika,
Vol. 70,
Issue. 2,
Hussain, Ayesha
and
Lamzouri, Youness
2024.
The limiting distribution of Legendre paths.
Journal de l’École polytechnique — Mathématiques,
Vol. 11,
Issue. ,
p.
589.
Harper, Adam J
2025.
A NOTE ON CHARACTER SUMS OVER SHORT MOVING INTERVALS.
Journal of the Institute of Mathematics of Jussieu,
p.
1.
GAO, PENG
and
ZHAO, LIANGYI
2025.
BOUNDS FOR MOMENTS OF QUADRATIC DIRICHLET CHARACTER SUMS.
Bulletin of the Australian Mathematical Society,
Vol. 111,
Issue. 1,
p.
43.