Published online by Cambridge University Press: 20 November 2018
Let A = [aij] denote an n-square matrix with entries in the field  of complex numbers. Denote by H a subgroup of Sn, the symmetric group on the integers 1, …, n, and by
of complex numbers. Denote by H a subgroup of Sn, the symmetric group on the integers 1, …, n, and by 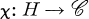 a character of degree 1 on H. Then
a character of degree 1 on H. Then
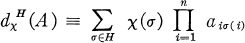
is the generalized matrix function of A associated with H and x; e.g., if H = Sn and χ = 1, then 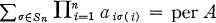 the permanent function. If the sequences ω = (ω1, …, ωm) and ϒ = (ϒ1, …, ϒm) are m-selections, m ≦ w, of integers 1, …, n, then A [ω| ϒ] denotes the m-square generalized submatrix [aωiϒj], i, j = 1, …, m, of the n-square matrix A. If ω is an increasing m-combination, then A [ω|ω] is an m-square principal submatrix of A.
the permanent function. If the sequences ω = (ω1, …, ωm) and ϒ = (ϒ1, …, ϒm) are m-selections, m ≦ w, of integers 1, …, n, then A [ω| ϒ] denotes the m-square generalized submatrix [aωiϒj], i, j = 1, …, m, of the n-square matrix A. If ω is an increasing m-combination, then A [ω|ω] is an m-square principal submatrix of A.