Hostname: page-component-78c5997874-g7gxr Total loading time: 0 Render date: 2024-11-05T05:43:20.641Z Has data issue: false hasContentIssue false
  • English
  • Français

A Mean Ergodic Theorem for Multiparameter Superadditive Processes on Banach Lattices

Published online by Cambridge University Press:  20 November 2018

Felix Lee
Felix Lee*
Affiliation:
Redeemer College, Ancaster, Ont L96 3N6
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let E be a Banach Lattice. We will consider E to be weakly sequentially complete and to have a weak unit u. Thus we may represent E as a lattice of real valued functions defined on a measure space (χ, 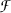, μ). There is a set R ⊂ χ such that R supports a maximal invariant function Φ for a postive contraction T on E [5]. Let N = χ — R be the complement of R. Akcoglu and Sucheston showed that 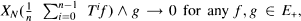where E+ is the positive cone of E. If in addition a monotone condition (UMB) is satisfied, then the same authors showed [4] that 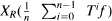converges in norm.

Keywords

47B5547A3528D05
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 42 , Issue 6 , 01 December 1990 , pp. 1018 - 1040
Copyright
Copyright © Canadian Mathematical Society 1990

References

1. Akcoglu, M. A. and Krengel, U., Ergodic theorems for superadditive processes. J. Reine Angew. Math. 323 (1981), pp. 53–67.Google Scholar
2. Akcoglu, M. A. and Krengel, U., and Sucheston, L., A ratio ergodic theorem for superadditive processes, Z. Wahrscheinlichkeitstheorie verw. Geb. 44 (1978), pp. 269–278.Google Scholar
3. Akcoglu, M. A. and Krengel, U., A stochastic ergodic theorem for superadditive processes, Ergodic Theory and Dynamic Systems. 3 (1983), pp. 335–344.Google Scholar
4. Akcoglu, M. A. and Krengel, U., A superadditive mean ergodic theorem on Banach lattices, J. of Mathematical Analysis and Application. 141 (1989), pp. 318–332.Google Scholar
5. Akcoglu, M. A. and Krengel, U., An ergodic theorem on Banach lattices, Israel J. Math. 57 (1985), pp. 208–222.Google Scholar
6. Akcoglu, M. A. and Krengel, U., On ergodic theory And truncated limits in Banach lattices, Proceedings of the 1983 Oberwolfach Measure Theory Conference, Lecture Notes in Math. 1089 (1984), Springer- Verlag, Berlin, pp. 241–262.Google Scholar
7. Akcoglu, M. A. and Krengel, U., On uniform ergodicity of norms and ergodic theorems injunction spaces, Supplemento ai Rendiconti del Circolo Mathematico di Palermo, Serie Il-numero 8, (1985), pp. 325–335.Google Scholar
8. Birkhoff, G., Lattice theory, AMS Colloquium Publications XXV, 3rd ed., (1967).Google Scholar
9. Derriennic, Y. and Krengel, U., Subadditive mean ergodic theorems. Ergodic Theory and Dynamic System, 7 (1981), pp. 33–48.Google Scholar
10. Kingman, J.F.C., Subadditive ergodic theory. Ann. Prob. 6 (1973), pp. 883–905.Google Scholar
11. Krengel, U., Ergodic theorems, de Gruyter studies in mathematics, Berlin, (1985).CrossRefGoogle Scholar
12. Lindenstrauss, J. and Tzafriri, L., Classical Banach spaces 11—Function Spaces, Springer-Verlag, Berlin, (1979).CrossRefGoogle Scholar
13. Millet, A. and Sucheston, L., On fixed points and multiparameter ergodic theorems for Banach lattices, Can. J. of Mathematics 40, (1988), pp. 429-158.Google Scholar
14. Schaffer, H.H., Banach lattices and positive operators. Springer-Verlag, New York, (1974).CrossRefGoogle Scholar
15. Smythe, R.T., Multiparameter subadditive processes. Annuals. Prob. 4 (1976), pp. 772–782.Google Scholar