Published online by Cambridge University Press: 08 February 2021
For a finite-dimensional Hopf algebra
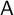 $\mathsf {A}$
, the McKay matrix
$\mathsf {A}$
, the McKay matrix
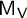 $\mathsf {M}_{\mathsf {V}}$
of an
$\mathsf {M}_{\mathsf {V}}$
of an
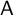 $\mathsf {A}$
-module
$\mathsf {A}$
-module
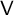 $\mathsf {V}$
encodes the relations for tensoring the simple
$\mathsf {V}$
encodes the relations for tensoring the simple
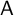 $\mathsf {A}$
-modules with
$\mathsf {A}$
-modules with
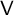 $\mathsf {V}$
. We prove results about the eigenvalues and the right and left (generalized) eigenvectors of
$\mathsf {V}$
. We prove results about the eigenvalues and the right and left (generalized) eigenvectors of
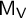 $\mathsf {M}_{\mathsf {V}}$
by relating them to characters. We show how the projective McKay matrix
$\mathsf {M}_{\mathsf {V}}$
by relating them to characters. We show how the projective McKay matrix
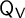 $\mathsf {Q}_{\mathsf {V}}$
obtained by tensoring the projective indecomposable modules of
$\mathsf {Q}_{\mathsf {V}}$
obtained by tensoring the projective indecomposable modules of
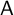 $\mathsf {A}$
with
$\mathsf {A}$
with
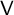 $\mathsf {V}$
is related to the McKay matrix of the dual module of
$\mathsf {V}$
is related to the McKay matrix of the dual module of
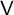 $\mathsf {V}$
. We illustrate these results for the Drinfeld double
$\mathsf {V}$
. We illustrate these results for the Drinfeld double
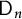 $\mathsf {D}_n$
of the Taft algebra by deriving expressions for the eigenvalues and eigenvectors of
$\mathsf {D}_n$
of the Taft algebra by deriving expressions for the eigenvalues and eigenvectors of
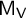 $\mathsf {M}_{\mathsf {V}}$
and
$\mathsf {M}_{\mathsf {V}}$
and
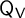 $\mathsf {Q}_{\mathsf {V}}$
in terms of several kinds of Chebyshev polynomials. For the matrix
$\mathsf {Q}_{\mathsf {V}}$
in terms of several kinds of Chebyshev polynomials. For the matrix
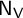 $\mathsf {N}_{\mathsf {V}}$
that encodes the fusion rules for tensoring
$\mathsf {N}_{\mathsf {V}}$
that encodes the fusion rules for tensoring
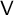 $\mathsf {V}$
with a basis of projective indecomposable
$\mathsf {V}$
with a basis of projective indecomposable
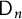 $\mathsf {D}_n$
-modules for the image of the Cartan map, we show that the eigenvalues and eigenvectors also have such Chebyshev expressions.
$\mathsf {D}_n$
-modules for the image of the Cartan map, we show that the eigenvalues and eigenvectors also have such Chebyshev expressions.