Hostname: page-component-cd9895bd7-7cvxr Total loading time: 0 Render date: 2024-12-25T05:59:47.291Z Has data issue: false hasContentIssue false
  • English
  • Français

The Maximum Modulus of Normal Meromorphic Functions and Applications to Value Distribution

Published online by Cambridge University Press:  20 November 2018

Paul Gauthier
Paul Gauthier*
Affiliation:
Université de Montréal, Montréal, Québec
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let f(z) be a function meromorphic in the unit disc D = (|z| < 1). We consider the maximum modulus

and the minimum modulus

When no confusion is likely, we shall write M(r) and m(r) in place of M(r,f) and m(r,f).

Since every normal holomorphic function belongs to an invariant normal family, a theorem of Hayman [6, Theorem 6.8] yields the following result.

THEOREM 1. If f(z) is a normal holomorphic function in the unit disc D, then

(1)

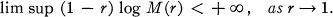
This means that for normal holomorphic functions, M(r) cannot grow too rapidly. The main result of this paper (Theorem 5, also due to Hayman, but unpublished) is that a similar situation holds for normal meromorphic functions.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 22 , Issue 4 , 01 August 1970 , pp. 803 - 814
Copyright
Copyright © Canadian Mathematical Society 1970

References

1. Gauthier, P. M., A criterion for normalcy, Nagoya Math. J. 32 (1968), 277–282.Google Scholar
2. Gauthier, P. M., Cercles de remplissage and asymptotic behaviour, Can. J. Math. 21 (1969), 447–455.Google Scholar
3. Gauthier, P. M., Cercles de remplissage and asymptotic behaviour along circuitous paths, Can. J. Math. 22 (1970), 389–393.Google Scholar
4. Gavrilov, V. I., On a theorem of A. L. Shaginjan, Vestnik Moskov. Univ. Ser I Mat. Meh., no. 2 (1966), 3–10. (Russian)Google Scholar
5. Hayman, W. K., On Nevanlinna1 s second theorem and extensions, Rend. Circ. Mat. Palermo (2) 2 (1953), 346–392.Google Scholar
5. Hayman, W. K., Meromorphic functions (Clarendon Press, Oxford, 1964).Google Scholar
7. Heins, M. H., The minimum modulus of a bounded analytic function, Duke Math. J. 14 (1947), 179–215.Google Scholar
8. Hille, E., Analytic function theory, Vol. 2 (Ginn, Boston, 1962).Google Scholar
9. Lange, L. H., Sur les cercles de remplissage non-euclidiens, Ann. Sci. Ecole Norm. Sup (3) 77 (1960), 257–280.Google Scholar
10. Rung, D. C., Behavior of holomorphic functions in the unit disc on arcs of positive hyperbolic diameter, J. Math. Kyoto Univ. 8 (1968), 417–464.Google Scholar
11. Schnitzer, F. and Seidel, W., On the rate with which a holomorphic function in a disk can tend radially to zero, Proc. Nat. Acad. Sci. U.S.A. 67 (1967), 876–877.Google Scholar
12. Shaginjan, A. L., A fundamental inequality in the theory of functions and its applications, Izv. Akad. Nauk Armjan. SSR Ser. Fiz.-Mat. Nauk 12 (1959), no. 1, 3–25. (Russian. Armenian Summary)Google Scholar
13. Walsh, J. L., Interpolation and approximation by rational functions in the complex domain, 3rd éd. (Amer. Math. Soc, Providence, Rhode Island, 1960).Google Scholar