Article contents
The Maximal p-Extension of a Local Field
Published online by Cambridge University Press: 20 November 2018
Extract
1. Let k denote a local field, that is, a complete discrete-valued field with perfect residue class field 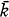 . Let G denote the Galois group of the maximal separable algebraic extension M of k, and let g denote the corresponding object over
. Let G denote the Galois group of the maximal separable algebraic extension M of k, and let g denote the corresponding object over 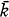 . For a given prime integer p, let G(p) denote the Galois group of the maximal p-extension of k. The dimensions of the cohomology groups
. For a given prime integer p, let G(p) denote the Galois group of the maximal p-extension of k. The dimensions of the cohomology groups
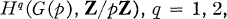
considered as vector spaces over the prime field Z/pZ, are equal, respectively, to the rank and the relation rank of the pro-p-group G(p); see [4; 9]. These dimensions are well known in many cases, especially when k is finite [6; 3; (Hoechsmann) 2, pp. 297-304], but also when k has characteristic p, or when k contains a primitive pth root of unity [4, p. 205].
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 1971
References
- 3
- Cited by


