Hostname: page-component-586b7cd67f-t7fkt Total loading time: 0 Render date: 2024-11-24T12:07:36.534Z Has data issue: false hasContentIssue false
  • English
  • Français

The Maximal Ideal Space of H∞ + C on the ball in Cn

Published online by Cambridge University Press:  20 November 2018

Gerard Mcdonald
Gerard Mcdonald*
Affiliation:
Michigan State University, East Lansing, Michigan
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let S denote the unit sphere in Cn, B the (open) unit ball in Cn and H∞(B) the collection of all bounded holomorphic functions on B. For f ∈ H∞(B) the limits

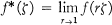
exist for almost every ζ in S, and the map ƒ → ƒ* defines an isometric isomorphism from H∞(B) onto a closed subalgebra of L∞(S), denoted H∞(S). (The only measure on S we will refer to in this paper is the Lebesgue measure, dσ, generated by Euclidean surface area.) Rudin has shown in [4] that the spaces H∞(B) + C(B) and H∞(S) + C(S) are Banach algebras in the sup norm. In this paper we will show that the maximal ideal space of H∞(B) + C(B), Σ (H∞(B) + C(B)), is naturally homeomorphic to Σ (H∞(B)) and that Z (H∞(S) + C(S)) is naturally homeomorphic to Σ (H∞(S))\B.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 31 , Issue 1 , 01 February 1979 , pp. 79 - 86
Copyright
Copyright © Canadian Mathematical Society 1979

References

1. Hoffman, K., Banach spaces of analytic functions (Prentice-Hall, Englewood Cliffs, N.J., 1962).Google Scholar
2. Kerzman, N., Holder and Lp estimates for solutions of du = f in strongly pseudoconvex domains, Comm. Pure Appl. Math. 24 (1971), 301–379.Google Scholar
3. Kerzman, N. and Nagel, A., Finitely generated ideals in certain function algebras, J. Functional Analysi. 7 (1971), 212–215.Google Scholar
4. Rudin, W., Spaces of type H∞ + C, Ann. Inst. Fourier (Grenoble) 25 (1975), 99–125.Google Scholar
5. Sarason, D. E., Generalized interpolation on Hx, Trans. Amer. Math. Soc. 127 (1967), 179–203.Google Scholar
6. Schark, I. J., The maximal ideals in an algebra of bounded analytic functions, J. Math. Mech. 10 (1961), 735–746.Google Scholar
7. Stein, E. M., Boundary behavior of holomorphic functions of several complex variables (Princeton University Press, Princeton, N.J., 1972).Google Scholar
8. Stout, E. L., The theory of uniform algebras (Bogden and Quigley, Tarrytown-on-Hudson, N.Y., 1971).Google Scholar