Hostname: page-component-586b7cd67f-2plfb Total loading time: 0 Render date: 2024-11-24T01:35:31.580Z Has data issue: false hasContentIssue false
  • English
  • Français

Matrices Whose Norms Are Determined by Their Actions on Decreasing Sequences

Published online by Cambridge University Press:  20 November 2018

Chang-Pao Chen ,
Hao-Wei Huang  and
Chun-Yen Shen
Chang-Pao Chen
Affiliation:
Department of Applied Mathematics, Hsuan Chuang University, Hsinchu 300, Taiwan, Republic of China e-mail:, [email protected]
Hao-Wei Huang
Affiliation:
Department of Mathematics, Indiana University, Bloomington, IN 47405, U.S.A. e-mail:, [email protected]:, [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 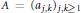$A={{({{a}_{j,k}})}_{j,k\ge 1}}$ be a non-negative matrix. In this paper, we characterize those 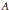$A$ for which 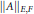${{\left\| A \right\|}_{E,F}}$ are determined by their actions on decreasing sequences, where 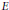$E$ and $F$ are suitable normed Riesz spaces of sequences. In particular, our results can apply to the following spaces: 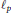${{\ell }_{p}}$, 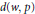$d(w,p)$, and 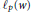${{\ell }_{p}}(w)$. The results established here generalize ones given by Bennett; Chen, Luor, and Ou; Jameson; and Jameson and Lashkaripour.

Keywords

15A6040G0547A3047B3746B42norms of matricesnormed Riesz spacesweighted mean matricesNörlund mean matricessummability matricesmatrices with row decreasing
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 60 , Issue 3 , 01 June 2008 , pp. 520 - 531
Copyright
Copyright © Canadian Mathematical Society 2008

References

[1] Ari˜no, M. A. and Muckenhoupt, B., A characterization of the dual of the classical Lorentz sequence space d(w, q). Proc. Amer.Math. Soc. 112(1991), no. 1, 87–89.Google Scholar
[2] Bennett, G., Some elementary inequalities. Quart. J. Math. Oxford 38(1987), no. 152, 401–425.Google Scholar
[3] Bennett, G., Inequalities complimentary to Hardy. Quart. J. Math. Oxford 49(1998), no. 196, 395–432.Google Scholar
[4] Boos, J., Classical and Modern Methods in Summability. Oxford University Press, New York, 2000.Google Scholar
[5] Chen, C.-P., Luor, D.-C., and Ou, Z.-Y., Extensions of Hardy inequality. J. Math. Anal. Appl. 273(2002), no. 1, 160–171.Google Scholar
[6] Jameson, G. J. O., Norms and lower bounds of operators on the Lorentz sequence space d(w, 1). Illinois J. Math. 43(1999), no. 1, 79–99.Google Scholar
[7] Jameson, G. J. O. and Lashkaripour, R., Lower bounds of operators on weighted ℓp spaces and Lorentz sequence spaces. Glasg. Math. J. 42(2000), no. 2, 211–223.Google Scholar
[8] Jameson, G. J. O. and Lashkaripour, R., Norms of certain operators on weighted ℓp spaces and Lorentz sequence spaces. J. Ineq. Pure Appl. Math. 3(2002), no. 1, 17 pp. (electronic)Google Scholar
[9] Meyer-Nieberg, P., Banach Lattices. Springer-Verlag, New York, 1991.Google Scholar
[10] Zygmund, A., Trigonometric Series. Vol. I, Second edition, Cambridge University Press, London, 1968.Google Scholar