Hostname: page-component-6bf8c574d5-vmclg Total loading time: 0 Render date: 2025-02-25T14:59:34.565Z Has data issue: false hasContentIssue false
  • English
  • Français

Markov's and Bernstein's Inequalities on Disjoint Intervals

Published online by Cambridge University Press:  20 November 2018

Peter B. Borwein
Peter B. Borwein*
Affiliation:
University of British Columbia, Vancouver, British Columbia
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In 1889, A. A. Markov proved the following inequality:

INEQUALITY 1. (Markov [4]). If pn is any algebraic polynomial of degree at most n then

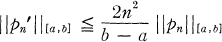
where ‖ ‖A denotes the supremum norm on A.

In 1912, S. N. Bernstein established

INEQUALITY 2. (Bernstein [2]). If pn is any algebraic polynomial of degree at most n then

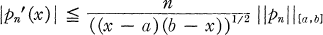
for x ∈ (a, b).

In this paper we extend these inequalities to sets of the form [a, b] ∪ [c, d]. Let Πn denote the set of algebraic polynomials with real coefficients of degree at most n.

THEOREM 1. Let a < b ≦ c < d and let pn ∈ Πn. Then

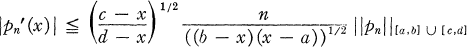
for x ∈ (a, b).

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 33 , Issue 1 , 01 February 1981 , pp. 201 - 209
Copyright
Copyright © Canadian Mathematical Society 1981

References

1. Achieser, N. L., Theory of approximation (Ungar, New York, 1956). (Translated from the Russian.)Google Scholar
2. Bernstein, S. N., Collected works, Akad. Nauk SSSR, Moscow 11 (1954).Google Scholar
3. Lorentz, G. G., Approximation of functions (Holt, Rinehart and Winston, New York, 1966).Google Scholar
4. Markov, A. A., On a problem of D. I. Mendeleev, Izv. Akad. Nauk 62 (1889), 1–24.Google Scholar
5. Soble, A. B., Majorants of polynomial derivatives, Amer. Math. Monthly 64 (1957), 639–643.Google Scholar