Hostname: page-component-cd9895bd7-dk4vv Total loading time: 0 Render date: 2024-12-28T17:15:19.036Z Has data issue: false hasContentIssue false
  • English
  • Français

Maps which Induce the Zero Map on Homotopy

Published online by Cambridge University Press:  20 November 2018

C. S. Hoo
C. S. Hoo*
Affiliation:
University of Alberta, Edmonton, Alberta
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In this paper, all spaces will have the homotopy type of simply connected CW-complexes, and will have base points which are preserved by maps and homotopies. We denote by [X, Y] the set of homotopy classes of maps from X to Y, and by N[X, Y] the subset of those homotopy classes [ƒ] which induce the zero homomorphism on homotopy, that is, 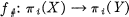is the zero homomorphism for each i.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 20 , 1968 , pp. 759 - 768
Copyright
Copyright © Canadian Mathematical Society 1968

References

1. Hu, S. T., Homotopy theory (Academic Press, New York, 1959).Google Scholar
2. Kahn, D. W., Induced maps for Postnikov systems, Trans. Amer. Math. Soc, 107 (1963), 432–450.Google Scholar
3. Kahn, D. W., Maps which induce the zero map on homotopy, Pacific J. Math., 15 (1965), 537–540.Google Scholar
4. Thomas, E., Homotopy classification of maps by cohomology homomorphisms, Trans. Amer. Math. Soc, 8 (1964), 138–151.Google Scholar
5. Thomas, E., Lectures on fibre spaces, Notes by J. McClendon (Springer-Verlag, New York, 1966).Google Scholar