Hostname: page-component-586b7cd67f-gb8f7 Total loading time: 0 Render date: 2024-11-24T07:01:38.247Z Has data issue: false hasContentIssue false
  • English
  • Français

Lushness, Numerical Index 1 and the Daugavet Property in Rearrangement Invariant Spaces

Published online by Cambridge University Press:  20 November 2018

Vladimir Kadets ,
Miguel Martín ,
Javier Merí  and
Dirk Werner
Vladimir Kadets
Affiliation:
Department of Mechanics and Mathematics, Kharkov National University, pl. Svobody 4, 61022 Kharkov, Ukraine, e-mail: [email protected]
Miguel Martín
Affiliation:
Departamento de Análisis Matematico, Facultad de Ciencias, Universidad de Granada, 18071 Granada, Spain, e-mail: [email protected], [email protected]
Javier Merí
Affiliation:
Departamento de Análisis Matematico, Facultad de Ciencias, Universidad de Granada, 18071 Granada, Spain, e-mail: [email protected], [email protected]
Dirk Werner
Affiliation:
Department of Mathematics, Freie Universitöt Berlin, Arnimallee 6, D-14 195 Berlin, Germany, e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

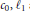We show that for spaces with 1–unconditional bases lushness, the alternative Daugavet property and numerical index 1 are equivalent. In the class of rearrangement invariant (r.i.) sequence spaces the only examples of spaces with these properties are ${{c}_{0,}}{{\ell }_{1}}$ and 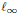${{\ell }_{\infty }}$. The only lush r.i. separable function space on 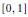$\left[ 0,1 \right]$ is 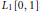${{L}_{1}}\left[ 0,1 \right]$; the same space is the only r.i. separable function space on 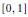$\left[ 0,1 \right]$ with the Daugavet property over the reals.

Keywords

46B0446E30lush spacenumerical indexDaugavet propertyKöthe spacerearrangement invariant space
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 65 , Issue 2 , 01 April 2013 , pp. 331 - 348
Copyright
Copyright © Canadian Mathematical Society 2013

References

[1] Acosta, M. D., Kamińska, A. and Mastyło, M., The Daugavet property and weak neighborhoods in Banach lattices. J. Convex Analysis, to appear.Google Scholar
[2] Avilés, A., Kadets, V.,Martín, M., Merí, J. and Shepelska, V., Slicely countably determined Banach spaces. C. R. Math. Acad. Sci. Paris 347(2009), 1277–1280.Google Scholar
[3] Avilés, A., Slicely countably determined Banach spaces. Trans. Amer. Math. Soc. 362(2010), 4871–4900.Google Scholar
[4] Bennett, C. and Sharpley, R., Interpolation of Operators. Pure Appl. Math. 129, Academic Press, Inc., New York, 1988.Google Scholar
[5] Bourgain, J. and Rosenthal, H. P., Martingales valued in certain subspaces of L1. Israel J. Math. 37(1980), 54–75. http://dx.doi.org/10.1007/BF02762868 Google Scholar
[6] Boyko, K., Kadets, V., Martín, M. and Werner, D., Numerical index of Banach spaces and duality. Math. Proc. Cambridge Philos Soc.. 142(2007), 93–102. http://dx.doi.org/10.1017/S0305004106009650 Google Scholar
[7] Duncan, J., McGregor, C., Pryce, J. and White, A., The numerical index of a normed space. J. London Math. Soc. 2(1970), 481–488.Google Scholar
[8] Ivakhno, Y. and Kadets, V., Unconditional sums of spaces with bad projections. Visn. Khark. Univ., Ser. Mat. Prykl. Mat. Mekh. 45 (2004), 30–35.Google Scholar
[9] Ivakhno, Y., Kadets, V. and Werner, D., The Daugavet property for spaces of Lipschitz functions. Math. Scand. 101(2007), 261–279; Corrigendum, Math. Scand. 104 (2009), 319.Google Scholar
[10] Kadets, V., Martín, M. and Merí, J., Norm equalities for operators on Banach spaces. Indiana Univ. Math. J. (2007), 2385–2411. http://dx.doi.org/10.1512/iumj.2007.56.3046 Google Scholar
[11] Kadets, V..Mart´ın, M., Merí, J., andPayá, R., Convexity and smoothness of Banach spaces with numerical index one. Illinois J. Math. 53(2009), 163–182.Google Scholar
[12] Kadets, V., Martín, M., Merí, J., and Shepelska, V., Lushness, numerical index one and duality. J. Math. Anal. Appl. 357(2009), 15–24. http://dx.doi.org/10.1016/j.jmaa.2009.03.055 Google Scholar
[13] Kadets, V., Shepelska, V. and Werner, D., Thickness of the unit sphere, ℓ1-types and the almost Daugavet property. Houston J. Math. 37(2011), 867–878.Google Scholar
[14] Kadets, V. and Shepelska, V., Sums of SCD sets and their applications to SCD operators and narrow operators. Cent. Eur. J. Math. 8(2010), 129–134. http://dx.doi.org/10.2478/s11533-009-0075-7 Google Scholar
[15] Kadets, V. M., Shvidkoy, R. V., Sirotkin, G. G. and Werner, D., Banach spaces with the Daugavet property. Trans. Amer. Math. Soc. 352(2000), 855–873. http://dx.doi.org/10.1090/S0002-9947-99-02377-6 Google Scholar
[16] Kadets, V. and Werner, D., A Banach space with the Schur and the Daugavet property. Proc. Amer. Math. Soc. 132(2004), 1765–1773. http://dx.doi.org/10.1090/S0002-9939-03-07278-2 Google Scholar
[17] Lindenstrauss, J. and Tzafriri, L., Classical Banach Spaces II. Springer-Verlag, Berlin-Heidelberg New York, 1979.Google Scholar
[18] Lee, H. J., Martín, M. and Merí, J., Polynomial numerical indices of Banach spaces with absolute norm. Linear Algebra Appl. 435(2011), 400–408. http://dx.doi.org/10.1016/j.laa.2011.01.037 Google Scholar
[19] M. Martín, and Oikhberg, T., An alternative Daugavet property. J. Math. Anal. Appl. 294(2004), 158–180. http://dx.doi.org/10.1016/j.jmaa.2004.02.006 Google Scholar
[20] Okada, S.,Ricker, W. J. and Sánchez Pérez, E. A., Optimal Domain and Integral Extension of Operators Acting in Function Spaces. Oper. Theory Adv. Appl. 180, Birkhäuser Verlag, Basel, 2008.Google Scholar
[21] Talagrand, M., The three-space problem for L1. J. Amer. Math. Soc. 3(1990), 9–29.Google Scholar