Hostname: page-component-cd9895bd7-8ctnn Total loading time: 0 Render date: 2024-12-19T01:52:05.705Z Has data issue: false hasContentIssue false
  • English
  • Français

Long Sets of Lengths With Maximal Elasticity

Published online by Cambridge University Press:  20 November 2018

Alfred Geroldinger  and
Qinghai Zhong
Alfred Geroldinger
Affiliation:
Institute for Mathematics and Scientiûc Computing, University of Graz, NAWI Graz, Heinrichstraße 36, 8010 Graz, Austria, e-mail: [email protected] , [email protected]
Qinghai Zhong
Affiliation:
Institute for Mathematics and Scientiûc Computing, University of Graz, NAWI Graz, Heinrichstraße 36, 8010 Graz, Austria, e-mail: [email protected] , [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We introduce a newinvariant describing the structure of sets of lengths in atomicmonoids and domains. For an atomic monoid $H$, let 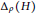${{\Delta }_{\rho }}\left( H \right)$ be the set of all positive integers d that occur as differences of arbitrarily long arithmetical progressions contained in sets of lengths havingmaximal elasticity 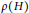$\rho \left( H \right)$. We study 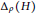${{\Delta }_{\rho }}\left( H \right)$ for transfer Krull monoids of finite type (including commutative Krull domains with finite class group) with methods from additive combinatorics, and also for a class of weakly Krull domains (including orders in algebraic number fields) for which we use ideal theoretic methods.

Keywords

13A0513F0516H1016U3020M13transfer Krull monoidweakly Krull monoidset of lengthelasticity
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 70 , Issue 6 , 01 December 2018 , pp. 1284 - 1318
Copyright
Copyright © Canadian Mathematical Society 2018

References

[1] Anderson, D. D., Anderson, D. E., and Zafrullah, M., Atomic domains in which almost all atoms are prime. Comm. Algebra 20 (1992), 1447–1462. http://dx.doi.Org/10.1080/00927879208824413Google Scholar
[2] Anderson, D. D., Mott, J., and Zafrullah, M., Finite character representations for integral domains. Boll. Un. Mat. Ital. B. 6 (1992), 613–630.Google Scholar
[3] Baeth, N. R. and Smertnig, D., Factorization theory: from commutative to noncommutative settings. J. Algebra 441 (2015), 475–551. http://dx.doi.Org/10.1016/j.jalgebra.2O15.06.007Google Scholar
[4] Barucci, V., D'Anna, M., and Frôberg, R., Analytically unramified one-dimensional semilocal rings and their value semigroups. J. Pure Appl. Algebra 147 (2000), 215–254. http://dx.doi.Org/10.1016/S0022-4049(98)00160-1Google Scholar
[5] Barucci, V., Dobbs, D. E., and Fontana, M., Maximality properties in numerical semigroups and applications to one-dimensional analytically irreducible local domains. Mem. Amer. Math. Soc, 125. 1997.Google Scholar
[6] Bowles, C., Chapman, S. T., Kaplan, N., and Reiser, D., On delta sets of numerical monoids. J. Algebra Appl. 5 (2006), 695–718. http://dx.doi.Org/10.1142/S0219498806001958Google Scholar
[7] Chang, S., Chapman, S. T., and Smith, W. W., On minimum delta set values in block monoids over cyclic groups. Ramanujan J. 14 (2007), 155–171. http://dx.doi.Org/10.1007/s11139-006-9000-xGoogle Scholar
[8] Chapman, S. T., Fontana, M., Geroldinger, A., and Olberding, B. (eds.), Multiplicative ideal theory and factorization theory. Springer Proceedings in Mathematics and Statistics, 170. Springer, 2016.Google Scholar
[9] Chapman, S. T., Holden, M., and Moore, T., Full elasticity in atomic monoids and integral domains. Rocky Mountain J. Math. 36 (2006), 1437–1455. http://dx.doi.Org/10.1216/rmjm/1181069375Google Scholar
[10] D'Anna, M., Ring and semigroup constructions. In: Multiplicative ideal theory and factorization theory. Springer Proc. Math. Stat, 170, Springer, 2016, pp. 97–115. http://dx.doi.Org/10.1007/978-3-319-38855-7_4Google Scholar
[11] Fan, Y. and Tringali, S., Power monoids: a bridge between factorization theory and arithmetic combinatorics. arxiv:1701.09152.Google Scholar
[12] Fan, Y. and Zhong, Q., Products ofk atoms in Krull monoids. Monatsh. Math. 181 (2016), 779–795. http://dx.doi.org/10.1007/s00605-016-0942-9Google Scholar
[13] Fontana, M., Houston, E., and Lucas, T., Factoring ideals in integral domains. Lecture Notes of the Unione Matematica Italiana, 14. Springer, Heidelberg, 2013.Google Scholar
[14] Geroldinger, A., On non-unique factorizations into irreducible elements. II. Colloq.Math. Soc. Janos Bolyai, 51. North Holland, Amsterdam, 1990, pp. 723-757.Google Scholar
[15] Geroldinger, A., Sets of lengths. Amer. Math. Monthly 123 (2016), 960–988.Google Scholar
[16] Geroldinger, A., Grynkiewicz, D. J., and Yuan, P., On products ofk atoms II. Mosc. J. Comb. Number Theory 5 (2015), 73–129.Google Scholar
[17] Geroldinger, A. and Halter-Koch, F., Non-unique factorizations, algebraic, combinatorial and analytic theory. Pure and Applied Mathematics, 278 Chapman and Hall/CRC, Boca Raton, FL, 2006.Google Scholar
[18] Geroldinger, A. and Kainrath, F., On the arithmetic of tame monoids with applications to Krull monoids and Mori domains. J. Pure Appl. Algebra 214 (2010), 2199–2218. http://dx.doi.org/!0.1016/j.jpaa.2O10.02.023Google Scholar
[19] Geroldinger, A., Kainrath, E., and Reinhart, A., Arithmetic of seminormal weakly Krull monoids and domains. J. Algebra 444 (2015), 201–245. http://dx.doi.Org/10.1016/j.jalgebra.2O15.07.026Google Scholar
[20] Geroldinger, A. and Schmid, W. A., A characterization of class groups via sets of lengths. arxiv:/1 503.04679Google Scholar
[21] Geroldinger, A., Schmid, W. A., and Zhong, Q., Systems of sets of lengths: transfer Krull monoids versus weakly Krull monoids. In: Rings, polynomials, and modules. Springer, 2017. arxiv:1 606.05063Google Scholar
[22] Geroldinger, A. and Yuan, P., The set of distances in Krull monoids. Bull. Lond. Math. Soc. 44 (2012), 1203–1208. http://dx.doi.Org/10.1112/blms/bds046Google Scholar
[23] Geroldinger, A. and Zhong, Q., The set of distances in seminormal weakly Krull monoids. J. Pure Appl. Algebra 220 (2016), 3713–3732. http://dx.doi.Org/10.1016/j.jpaa.2O16.05.009Google Scholar
[24] Geroldinger, A. and Zhong, Q., The set of minimal distances in Krull monoids. Acta Arith. 173 (2016), 97–120.Google Scholar
[25] Geroldinger, A. and Zhong, Q., A characterization of class groups via sets of lengths II. J. Théor. Nombres Bordeaux. 29 (2017), 327–346.Google Scholar
[26] Halter-Koch, F., Divisor theories with primary elements and weakly Krull domains. Boll. Un. Mat. Ital. B 9 (1995), 417–441.Google Scholar
[27] Halter-Koch, F., Elasticity of factorizations in atomic monoids and integral domains. J. Théor. Nombres Bordeaux. 7 (1995), 367–385. http://dx.doi.Org/10.58O2/jtnb.147Google Scholar
[28] Halter-Koch, F., Ideal systems. An introduction to multiplicative ideal theory. Monographs and Textbooks in Pure and Applied Mathematics, 211. Marcel Dekker, New York, 1998.Google Scholar
[29] Halter-Koch, F., Quadratic Irrationals. Pure and Applied Mathematics, 306. Chapman and Hall/CRC, Boca Ration, FL, 2013.Google Scholar
[30] Kainrath, F., A note on quotients formed by unit groups of semilocal rings. Houston J. Math. 24 (1998), 613–618.Google Scholar
[31] Kainrath, F., Arithmetic of Mori domains and monoids: the global case. In: Multiplicative ideal theory and factorization theory. Springer Proc. Math. Stat., 170. Springer, 2016, pp. 183–218.Google Scholar
[32] Plagne, A. and Schmid, W. A., On congruence half-factorial Krull monoids with cyclic class group. arxiv:1 709.00859Google Scholar
[33] Schmid, W. A., The inverse problem associated to the Davenport constant for C2 ⊕ C2 ⊕ C2n, and applications to the arithmetical characterization of class groups. Electron. J. Comb. 18 (2011), Research Paper 33.Google Scholar
[34] Schmid, W. A., Some recent results and open problems on sets of lengths of Krull monoids with finite class group. In: Multiplicative ideal theory and factorization theory. Springer Proc. Math. Stat., 170. Springer, 2016, pp. 323–352.Google Scholar
[35] Smertnig, D., Factorizations in bounded hereditary noetherianprime rings. arxiv:1605.09274Google Scholar
[36] Smertnig, D., Sets of lengths in maximal orders in central simple algebras. J. Algebra 390 (2013), 1–43. http://dx.doi.Org/10.1016/j.jalgebra.2013.05.016Google Scholar
[37] Zhong, Q., Sets of minimal distances and characterizations of class groups of Krull monoids. Ramanujan J., to appear.Google Scholar