Hostname: page-component-586b7cd67f-2plfb Total loading time: 0 Render date: 2024-12-01T04:35:08.691Z Has data issue: false hasContentIssue false
  • English
  • Français

Locally Flat Vector Lattices

Published online by Cambridge University Press:  20 November 2018

Marlow Anderson
Marlow Anderson*
Affiliation:
Purdue University at Fort Wayne, Fort Wayne, Indiana
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let G be a lattice-ordered group (l-group). If X ⊆ G, then let

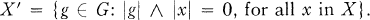
Then X’ is a convex l-subgroup of G called a polar. The set P(G) of all polars of G is a complete Boolean algebra with ‘ as complementation and set-theoretic intersection as meet. An l-subgroup H of G is large in G (G is an essential extension of H) if each non-zero convex l-subgroup of G has non-trivial intersection with H. If these l-groups are archimedean, it is enough to require that each non-zero polar of G meets H. This implies that the Boolean algebras of polars of G and H are isomorphic. If K is a cardinal summand of G, then K is a polar, and we write G = K⊞K'.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 32 , Issue 4 , April 1980 , pp. 924 - 936
Copyright
Copyright © Canadian Mathematical Society 1980

References

1. Anderson, M., The essential closure of C(X), Proc. AMS 76 (1979), 8–10.Google Scholar
2. Bigard, A., Keimel, K. and Wolfenstein, S., Groupes et anneaux réticulés (Springer-Verlag, Berlin, 1977).CrossRefGoogle Scholar
3. Conrad, P., Archimedean extensions of lattice-ordered groups, J. Indian Math. Soc. 30 (1966), 131–160.Google Scholar
4. Conrad, P., Lattice-ordered groups, Tulane Lecture Notes (1970).Google Scholar
5. Conrad, P., Epi-archimedean groups, Czech. Math. J. 24 (1974), 192–218.Google Scholar
6. Gillman, L. and Jerison, M., Rings of continuous functions (Van Nostrand Reinhold, New York, 1960).CrossRefGoogle Scholar
7. Iliadis, S. and Fomin, S., The method of centred systems in the theory of topological spaces, Uspekhi Mat. Nank 21 (1966), 47–76. English translation: Russian Math. Surveys 21 (1966), 37–62.Google Scholar
8. Porter, J. and Woods, R. G., Minimal extremally disconnected Hausdorff spaces, Gen. Top. and Appl. 8 (1978), 9–26.Google Scholar
9. Šik, F., Closed and open sets in topologies induced by lattice ordered vector groups, Czech. Math. J. 23 (1973), 139–150.Google Scholar