Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Alexander, Stephanie
and
Ghomi, Mohammad
2003.
The convex hull property and topology of hypersurfaces with nonnegative curvature.
Advances in Mathematics,
Vol. 180,
Issue. 1,
p.
324.
Rybnikov, Konstantin
2008.
On convexity of hypersurfaces in the hyperbolic space.
Geometriae Dedicata,
Vol. 136,
Issue. 1,
p.
123.
Rybnikov, Konstantin
2009.
An efficient local approach to convexity testing of piecewise-linear hypersurfaces.
Computational Geometry,
Vol. 42,
Issue. 2,
p.
147.
Ghomi, Mohammad
and
Xiong, Changwei
2019.
Nonnegatively curved hypersurfaces with free boundary on a sphere.
Calculus of Variations and Partial Differential Equations,
Vol. 58,
Issue. 3,


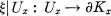 is a homeomorphism onto its image. We shall call such a mapping ξ a
is a homeomorphism onto its image. We shall call such a mapping ξ a 