Hostname: page-component-78c5997874-g7gxr Total loading time: 0 Render date: 2024-11-02T22:16:18.525Z Has data issue: false hasContentIssue false
  • English
  • Français

Localization in Categories of Complexes and Unbounded Resolutions

Published online by Cambridge University Press:  20 November 2018

Leovigildo Alonso Tarrío ,
Ana Jeremías López  and
María José Souto Salorio
Leovigildo Alonso Tarrío
Affiliation:
Departamento de Álxebra, Facultade de Matemáticas, Universidade de Santiago de Compostela, E-15771 Santiago de Compostela, Spain email: [email protected]
Ana Jeremías López
Affiliation:
Departamento de Álxebra, Facultade de Matemáticas, Universidade de Santiago de Compostela, E-15771 Santiago de Compostela, Spain email: [email protected]
María José Souto Salorio
Affiliation:
Facultade de Informática, Campus de Elviña, Universidade da Coruña, E-15071 A Coruña, Spain email: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

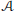In this paper we show that for a Grothendieck category $\mathcal{A}$ and a complex 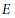$E$ in 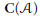$\mathbf{C}(\mathcal{A})$ there is an associated localization endofunctor 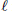$\ell$ in 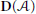$\mathbf{D}(\mathcal{A})$. This means that 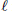$\ell$ is idempotent (in a natural way) and that the objects that go to 0 by 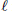$\ell$ are those of the smallest localizing (= triangulated and stable for coproducts) subcategory of 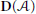$\mathbf{D}(\mathcal{A})$ that contains 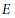$E$. As applications, we construct 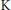$\text{K}$-injective resolutions for complexes of objects of 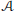$\mathcal{A}$ and derive Brown representability for 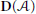$\mathbf{D}(\mathcal{A})$ from the known result for 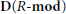$\mathbf{D}(R-\mathbf{mod})$, where 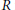$R$ is a ring with unit.

Keywords

18E3018E1518E35
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 52 , Issue 2 , 01 April 2000 , pp. 225 - 247
Copyright
Copyright © Canadian Mathematical Society 2000

References

[AJL] Tarrío, Leovigildo Alonso, López, Ana Jeremías and Lipman, Joseph, Local homology and cohomology on schemes. Ann. Sci. École Norm. Sup. (4) 30(1997), 1–39.Google Scholar
[BBD] Beĭlinson, A. A., Bernstein, J. and Deligne, P., Faisceaux pervers. Analysis and topology on singular spaces, I (Luminy, 1981), 5–171; Astérisque 100, Soc. Math. France, Paris, 1982.Google Scholar
[BN] Bökstedt, Marcel and Neeman, Amnon, Homotopy limits in triangulated categories. Compositio Math. (2) 86(1993), 209–234.Google Scholar
[Bo1] Bousfield, A. K., The localization of spectra with respect to homology. Topology (4) 18(1979), 257–281.Google Scholar
[Bo2] Bousfield, A. K., The Boolean algebra of spectra. Comment.Math. Helv. (3) 54(1979), 368–377.Google Scholar
[Bo2a] Bousfield, A. K., Correction to: “The Boolean algebra of spectra”. Comment.Math. Helv. (4) 58(1983), 599–600.Google Scholar
[BK] Bousfield, A. K. and Kan, D. M., Homotopy limits, completions and localizations. LectureNotes in Math. 304, Springer-Verlag, Berlin-New York, 1972.Google Scholar
[CtHK] Colliot-Thélène, Jean-Louis, Hoobler, Raymond T. and Kahn, Bruno, The Bloch-Ogus-Gabber theorem. In: Algebraic K-theory (Toronto, ON, 1996), Amer. Math. Soc., Providence, RI, 1998, 31–94.Google Scholar
[F] Franke, J., On the Brown representability theorem for triangulated categories. Preprint.Google Scholar
[GP] Popesco, Nicolae and Gabriel, Pierre, Caractérisation des catégories abéliennes avec générateurs et limites inductives exactes. C. R. Acad. Sci. Paris 258(1964), 4188–4190.Google Scholar
[I] Iversen, Birger, Cohomology of sheaves. Universitext. Springer-Verlag, Berlin-New York, 1986.Google Scholar
[K] Keller, Bernhard, Deriving DG categories. Ann. Sci. École Norm. Sup. (4) 27(1994), 63–102.Google Scholar
[L] Lévy, Azriel, Basic set theory. Springer-Verlag, Berlin-New York, 1979.Google Scholar
[N1] Neeman, Amnon, The connection between the K-theory localization theorem of Thomason, Trobaugh and Yao and the smashing subcategories of Bousfield and Ravenel. Ann. Sci. École Norm. Sup. (4) 25(1992), 547–566.Google Scholar
[N2] Neeman, Amnon, The chromatic tower for D(R). Topology (3) 31(1992), 519–532.Google Scholar
[N3] Neeman, Amnon, The Grothendieck duality theoremvia Bousfield's techniques and Brown representability. J. Amer. Math. Soc. (1) 9(1996), 205–236.Google Scholar
[N4] Neeman, Amnon, Triangulated categories. Book in preparation.Google Scholar
[P] Puppe, Dieter, On the formal structure of stable homotopy theory. Colloq. algebr. Topology, Aarhus, 1962, 65–71.Google Scholar
[Ri] Rickard, Jeremy, Derived categories and stable equivalence. J. Pure Appl. Algebra (3) 61(1989), 303–317.Google Scholar
[Sp] Spaltenstein, N., Resolutions of unbounded complexes. Compositio Math. (2) 65(1988), 121–154.Google Scholar
[St] Stenström, Bo, Rings of quotients. An introduction to methods of ring theory. GrundlehrenMath. Wiss. 217. Springer-Verlag, Berlin-Heidelberg-New York, 1975.Google Scholar
[Ve] Verdier, Jean-Louis, Catégories dérivées. Quelques résultats (Etat 0). Sémin. Géom. algébr. Bois-Marie, SGA 4½, LectureNotes in Math. 569(1977), 262–311.Google Scholar
[W] Weibel, Charles A., An introduction to homological algebra. Cambridge Stud. Adv. Math. 38. Cambridge University Press, Cambridge, 1994.Google Scholar