Article contents
A Local Ergodic Theorem on Lp
Published online by Cambridge University Press: 20 November 2018
Extract
Two general types of pointwise ergodic theorems have been studied: those as t approaches infinity, and those as t approaches zero. This paper deals with the latter case, which is referred to as the local case.
Let (X, 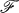 , μ) be a complete, σ-finite measure space. Let {Tt} be a strongly continuous one-parameter semi-group of contractions on
, μ) be a complete, σ-finite measure space. Let {Tt} be a strongly continuous one-parameter semi-group of contractions on 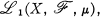 , defined for t ≧ 0. For Tt positive, it was shown independently in [2] and [5] that
, defined for t ≧ 0. For Tt positive, it was shown independently in [2] and [5] that
1.1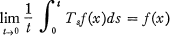
almost everywhere on X, for any f ∊ L1. The same result was obtained in [1], with the continuity assumption weakened to having it hold for t > 0.
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 1974
References
- 2
- Cited by


