Local Convergence and Stability of Tight Bridge-addable Classes

Abstract

A class of graphs is bridge-addable if given a graph 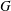$G$ in the class, any graph obtained by adding an edge between two connected components of 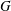$G$ is also in the class. The authors recently proved a conjecture of McDiarmid, Steger, and Welsh stating that if 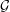${\mathcal{G}}$ is bridge-addable and 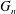$G_{n}$ is a uniform $n$-vertex graph from 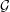${\mathcal{G}}$, then 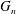$G_{n}$ is connected with probability at least 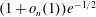$(1+o_{n}(1))e^{-1/2}$. The constant 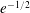$e^{-1/2}$ is best possible, since it is reached for the class of all forests.

In this paper, we prove a form of uniqueness in this statement: if 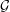${\mathcal{G}}$ is a bridge-addable class and the random graph 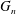$G_{n}$ is connected with probability close to 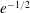$e^{-1/2}$, then 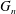$G_{n}$ is asymptotically close to a uniform $n$-vertex random forest in a local sense. For example, if the probability converges to 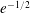$e^{-1/2}$, then 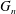$G_{n}$ converges in the sense of Benjamini–Schramm to the uniformly infinite random forest 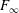$F_{\infty }$. This result is reminiscent of so-called “stability results” in extremal graph theory, the difference being that here the stable extremum is not a graph but a graph class.