Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Askey, Richard
and
Gasper, George
1971.
Jacobi polynomial expansions of Jacobi polynomials with non-negative coefficients.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 70,
Issue. 2,
p.
243.
Gasper, George
1971.
A Positive Integral (Richard Askey).
SIAM Review,
Vol. 13,
Issue. 3,
p.
396.
Askey, Richard
and
Gasper, George
1972.
Certain Rational Functions Whose Power Series Have Positive Coefficients.
The American Mathematical Monthly,
Vol. 79,
Issue. 4,
p.
327.
Dunkl, Charles F.
1973.
The measure algebra of a locally compact hypergroup.
Transactions of the American Mathematical Society,
Vol. 179,
Issue. 0,
p.
331.
Askey, Richard
1974.
Certain Rational Functions Whose Power Series Have Positive Coefficients. II.
SIAM Journal on Mathematical Analysis,
Vol. 5,
Issue. 1,
p.
53.
Gasper, George
1975.
Theory and Application of Special Functions.
p.
375.
Rahman, M.
1976.
Construction of a Family of Positive Kernels from Jacobi Polynomials.
SIAM Journal on Mathematical Analysis,
Vol. 7,
Issue. 1,
p.
92.
Askey, R.
and
Bingham, N. H.
1976.
Gaussian processes on compact symmetric spaces.
Zeitschrift f�r Wahrscheinlichkeitstheorie und Verwandte Gebiete,
Vol. 37,
Issue. 2,
p.
127.
Koornwinder, Tom
and
Sprinkhuizen-Kuyper, Ida
1978.
Generalized Power Series Expansions for a Class of Orthogonal Polynomials in Two Variables.
SIAM Journal on Mathematical Analysis,
Vol. 9,
Issue. 3,
p.
457.
Flensted-Jensen, Mogens
and
Koornwinder, Tom H.
1979.
Jacobi functions: The addition formula and the positivity of the dual convolution structure.
Arkiv för Matematik,
Vol. 17,
Issue. 1-2,
p.
139.
Cazzaniga, Franco
and
Meaney, Christopher
1982.
A local property of absolutely convergent Jacobi polynomial series.
Tohoku Mathematical Journal,
Vol. 34,
Issue. 3,
Kanjin, Yûichi
1984.
On the algebra of absolutely convergent disk polynomial series.
Proceedings of the Japan Academy, Series A, Mathematical Sciences,
Vol. 60,
Issue. 9,
Kanjin, Yūichi
1985.
Banach algebra related to disk polynomials.
Tohoku Mathematical Journal,
Vol. 37,
Issue. 3,
Rahman, Mizan
and
Shah, Mihr J.
1985.
An Infinite Series with Products of Jacobi Polynomials and Jacobi Functions of the Second Kind.
SIAM Journal on Mathematical Analysis,
Vol. 16,
Issue. 4,
p.
859.
Lasser, R.
and
Leitner, M.
1990.
On the estimation of the mean of weakly stationary and polynomial weakly stationary sequences.
Journal of Multivariate Analysis,
Vol. 35,
Issue. 1,
p.
31.
Szwarc, Ryszard
1992.
Orthogonal Polynomials and a Discrete Boundary Value Problem II.
SIAM Journal on Mathematical Analysis,
Vol. 23,
Issue. 4,
p.
965.
Szwarc, Ryszard
1992.
Orthogonal Polynomials and a Discrete Boundary Value Problem I.
SIAM Journal on Mathematical Analysis,
Vol. 23,
Issue. 4,
p.
959.
Levenshtein, V. I.
1992.
Designs as maximum codes in polynomial metric spaces.
Acta Applicandae Mathematicae,
Vol. 29,
Issue. 1-2,
p.
1.
Szwarc, Ryszard
1992.
Convolution structures associated with orthogonal polynomials.
Journal of Mathematical Analysis and Applications,
Vol. 170,
Issue. 1,
p.
158.
Askey, Richard
1993.
Problems which interest and/or annoy me.
Journal of Computational and Applied Mathematics,
Vol. 48,
Issue. 1-2,
p.
3.


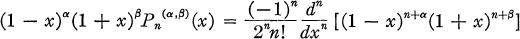
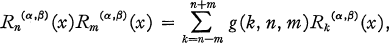
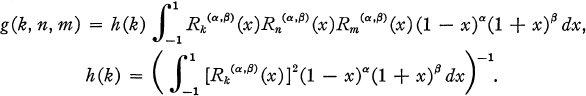
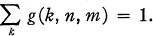
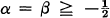 (the ultraspherical case) or if
(the ultraspherical case) or if 