Linear stability of the regular N-gon periodic solutions for the planar N-body problem with quasi-homogeneous potential

Abstract

This paper considers the planar N-body problem with a quasi-homogeneous potential given by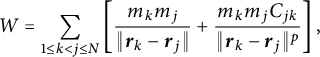

$$ \begin{align*}W = \sum_{1\leq k<j\leq N} \left[ \frac{ m_k m_j}{\|\boldsymbol{r}_k-\boldsymbol{r}_j\|} +\frac{m_k m_j C_{jk}}{\|\boldsymbol{r}_k-\boldsymbol{r}_j\|^p} \right], \end{align*} $$

where 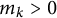$ m_k>0 $ are the masses and 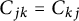$C_{jk}= C_{kj}$ are nonzero real constants, and the exponent g being 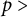$ p> $1. Generalizing techniques of the classical N-body problem, we first characterize the periodic solutions that form a regular polygon (relative equilibria) with equal masses (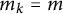$m_k= m$, 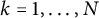$k=1, \ldots , N$) and equal constants 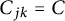$C_{jk}= C$, for all 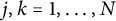$j, k=1, \ldots , N$ (for short, N-gon solutions). Indeed, for 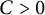$C>0$ we prove that there exists a unique regular N-gon solution for each fixed positive mass m. In contrast, for the case 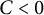$C <0$, we demonstrate that there can be a maximum of two distinct regular N-gon solutions for a fixed positive mass m. More precisely, there is a range of values for the mass parameter m for which no solutions of the form of an N-gon exist. Furthermore, we examine the linear stability of these solutions, with a particular focus on the special case 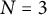$ N=3 $, which is fully characterized.