Hostname: page-component-cd9895bd7-jn8rn Total loading time: 0 Render date: 2025-01-02T14:15:47.829Z Has data issue: false hasContentIssue false
  • English
  • Français

Linear homeomorphisms of function spaces and the position of a space in its compactification

Part of: Maps and general types of spaces defined by maps Fairly general properties Linear function spaces and their duals Basic constructions Game theory

Published online by Cambridge University Press:  28 November 2023

Mikołaj Krupski Open the ORCID record for Mikołaj Krupski [Opens in a new window]
Mikołaj Krupski*
Affiliation:
Institute of Mathematics, University of Warsaw, Warszawa, Poland
*
e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

An old question of Arhangel’skii asks if the Menger property of a Tychonoff space X is preserved by homeomorphisms of the space 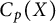$C_p(X)$ of continuous real-valued functions on X endowed with the pointwise topology. We provide affirmative answer in the case of linear homeomorphisms. To this end, we develop a method of studying invariants of linear homeomorphisms of function spaces 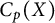$C_p(X)$ by looking at the way X is positioned in its (Čech–Stone) compactification.

Keywords

Function spacepointwise convergence topologyMenger spaceHurewicz spacelinear homeomorphism

MSC classification

Primary: 46E10: Topological linear spaces of continuous, differentiable or analytic functions 54C35: Function spaces 54D20: Noncompact covering properties (paracompact, Lindelöf, etc.) 54D40: Remainders
Secondary: 54C60: Set-valued maps 54B20: Hyperspaces 91A44: Games involving topology or set theory
Type
Article
Information
Canadian Journal of Mathematics , Volume 76 , Issue 6 , December 2024 , pp. 2151 - 2172
Check for updates
Copyright
© The Author(s), 2023. Published by Cambridge University Press on behalf of The Canadian Mathematical Society

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

The author was partially supported by the NCN (National Science Centre, Poland) research Grant No. 2020/37/B/ST1/02613.

References

Arhangel’skii, A. V., Linear homeomorphisms of function spaces . Dokl. Akad. Nauk SSSR 264(1982), no. 6, 1289–1292.Google Scholar
Arkhangel’skiĭ, A. V., Topological function spaces, Mathematics and Its Applications (Soviet Series), 78, Kluwer Academic, Dordrecht, 1992.CrossRefGoogle Scholar
Aurichi, L. F. and Dias, R. R., A minicourse on topological games . Topology Appl. 258(2019), 305–335.CrossRefGoogle Scholar
Banakh, T. and Zdomskyy, L., Separation properties between the $\sigma$ -compactness and Hurewicz property . Topology Appl. 156(2008), no. 1, 10–15.CrossRefGoogle Scholar
Bonanzinga, M., Cammaroto, F., and Matveev, M., Projective versions of selection principles . Topology Appl. 157(2010), no. 5, 874–893.CrossRefGoogle Scholar
Bouziad, A., Consonance and topological completeness in analytic spaces . Proc. Amer. Math. Soc. 127(1999), no. 12, 3733–3737.CrossRefGoogle Scholar
Bouziad, A., Le degré de Lindelöf est $l$ -invariant . Proc. Amer. Math. Soc. 129(2001), no. 3, 913–919.CrossRefGoogle Scholar
Dolecki, S., Greco, G. H., and Lechicki, A., When do the upper Kuratowski topology (homeomorphically, Scott topology) and the co-compact topology coincide? Trans. Amer. Math. Soc. 347(1995), no. 8, 2869–2884.CrossRefGoogle Scholar
Engelking, R., General topology, 2nd ed., Sigma Series in Pure Mathematics, 6, Heldermann, Berlin, 1989.Google Scholar
Just, W., Miller, A. W., Scheepers, M., and Szeptycki, P. J., The combinatorics of open covers. II . Topology Appl. 73(1996), no. 3, 241–266.CrossRefGoogle Scholar
Kočinac, L. D. R., Selection principles and continuous images . Cubo 8(2006), no. 2, 23–31.Google Scholar
Krupski, M., On the $t$ -equivalence relation . Topology Appl. 160(2013), no. 2, 368–373.CrossRefGoogle Scholar
Krupski, M., Games and hereditary Baireness in hyperspaces and spaces of probability measures . J. Inst. Math. Jussieu 21(2022), no. 3, 851–868.CrossRefGoogle Scholar
Krupski, M. and Kucharski, K., Some remarks on the projective properties of Menger and Hurewicz. Preprint, 2023. arXiv:2302.12933 [math.GN]CrossRefGoogle Scholar
Okunev, O., Weak topology of a dual space and a $t$ -equivalence relation . Mat. Zametki 46(1989), no. 1, 53–59, 123.Google Scholar
Okunev, O., A relation between spaces implied by their $t$ -equivalence . Topology Appl. 158(2011), no. 16, 2158–2164.CrossRefGoogle Scholar
Porada, E., Jeu de Choquet . Colloq. Math. 42(1979), 345–353.CrossRefGoogle Scholar
Sakai, M., The Menger property and $l$ -equivalence . Topology Appl. 281(2020), Article no. 107187, 6 pp.CrossRefGoogle Scholar
Sakai, M. and Scheepers, M., The combinatorics of open covers . In: Recent progress in general topology. III, Atlantis Press, Paris, 2014, pp. 751–799.CrossRefGoogle Scholar
Scheepers, M., Combinatorics of open covers. I. Ramsey theory . Topology Appl. 69(1996), no. 1, 31–62.CrossRefGoogle Scholar
Smirnov, Y. M., On normally disposed sets of normal spaces . Mat. Sbornik N.S. 29(1951), no. 71, 173–176.Google Scholar
Tall, F. D., Lindelöf spaces which are Menger, Hurewicz, Alster, productive, or $D$ . Topology Appl. 158(2011), no. 18, 2556–2563.CrossRefGoogle Scholar
Telgársky, R., On games of Topsøe . Math. Scand. 54(1984), no. 1, 170–176.CrossRefGoogle Scholar
Tkachuk, V. V., A Cp-theory problem book. Functional equivalencies, Problem Books in Mathematics, Springer, Cham, 2016.CrossRefGoogle Scholar
Valov, V., Spaces of bounded functions with the compact open topology . Bull. Polish Acad. Sci. Math. 45(1997), no. 2, 171–179.Google Scholar
Valov, V., Spaces of bounded functions . Houst. J. Math. 25(1999), no. 3, 501–521.Google Scholar
van Mill, J., The infinite-dimensional topology of function spaces, North-Holland Mathematical Library, 64, North-Holland, Amsterdam, 2001.Google Scholar
Velichko, N. V., The Lindelöf property is $l$ -invariant . Topology Appl. 89(1998), no. 3, 277–283.CrossRefGoogle Scholar
Zdomskyy, L., $o$ -boundedness of free objects over a Tychonoff space . Mat. Stud. 25(2006), no. 1, 10–28.Google Scholar