Hostname: page-component-cd9895bd7-dk4vv Total loading time: 0 Render date: 2024-12-25T06:36:16.720Z Has data issue: false hasContentIssue false
  • English
  • Français

Linear Combinations of Univalent Functions with Complex Coefficients

Published online by Cambridge University Press:  20 November 2018

Robert K. Stump
Robert K. Stump*
Affiliation:
Muhlenberg College, Allentown, Pennsylvania
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let U be the class of all normalized analytic functions

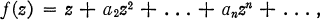
where z ∈ E = {z : |z| < 1} and ƒ is univalent in E. Let K denote the sub-class of U consisting of those members that map E onto a convex domain. MacGregor [2] showed that if ƒ1 ∈ K and ƒ2 ∈ K and if

1

then F ∉ K when λ is real and 0 < λ < 1, and the radius of univalency and starlikeness for F is .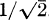

In this paper, we examine the expression (1) when ƒ1 ∈ K, ƒ2 ∈ K and λ is a complex constant and find the radius of starlikeness for such a linear combination of complex functions with complex coefficients.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 23 , Issue 4 , August 1971 , pp. 712 - 717
Copyright
Copyright © Canadian Mathematical Society 1971

References

1. Labelle, G. and Rahman, Q. I., Remarque sur La moyenne arithmétique de Jonctions univalentes convexes, Can. J. Math. 21 (1969), 977–981.Google Scholar
2. MacGregor, T. H., The univalence of a linear combination of convex mappings, J. London Math. Soc. 44 (1969), 210–212.Google Scholar
3. Marx, A., Untersuchungen uber schlichte Abbildungen, Math. Ann. 107 (1932), 40–67.Google Scholar
4. Strohhäcker, E., Beitrage zur Théorie der schlichte Funktionen, Math. Z. 37 (1933). 356–380.Google Scholar