Hostname: page-component-cd9895bd7-mkpzs Total loading time: 0 Render date: 2024-12-25T05:45:29.687Z Has data issue: false hasContentIssue false
  • English
  • Français

Limits on Pairwise Amicable Orthogonal Designs

Published online by Cambridge University Press:  20 November 2018

Warren Wolfe
Warren Wolfe*
Affiliation:
Royal Roads, Mutiary College, Victoria, British Columbia
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

An orthogonal design in order n of type (u1, …, ut) on the commuting variables x1, …, xt is an n × n matrix X with entries 0, ±x1, …, ±xt such that

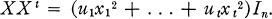
In [5] Geramita and Wallis show that if n = 24a+b·n0, where n0 is odd and 0 ≦ b > 4, then t ≧ ρ(n) = 8a + 2b. The result is essentially Radon's limit on the number of anti-commuting, real, anti-symmetric, orthogonal matrices in order n. Garamita and Pullman show that this limit is sharp for orthogonal designs: i.e., given n, there exists an orthogonal design in order n with ρ(n) variables [6].

Two orthogonal designs, X and F, are called amicable if XYt = YXt.

Such pairs of orthogonal designs are especially useful in generating new orthogonal designs [5] or [6].

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 33 , Issue 5 , 01 October 1981 , pp. 1043 - 1054
Copyright
Copyright © Canadian Mathematical Society 1981

References

1. Dornhoff, L., Group representation theory, part A (Marrel Dekker, New York, 1971).Google Scholar
2. Eckmann, B., Gruppentheoretischer Bewis des Satzes von Hurwitz-Radon über die Komposition quadratischer Formen. Comment, Math. Elelv. 15 (1943).Google Scholar
3. Isaacs, I. M., Character theory of finite groups (Academic Press, New York, 1976).Google Scholar
4. Herstein, J. N., Non-commutative rings, Carus Math, Mono. 15, M.A.A. (Wiley, New York, 1968).Google Scholar
5. Geramita, A. V., Geramita, J. M. and Wallis, J. S., Orthogonal designs, J. Linear and Multilinear Alg. 3 (1975/76).Google Scholar
6. Geramita, A. V. and Pullman, N. J., A theorem of Hurwitz and Radon and orthogonal projective modules, Proc. A.M.S. 42 (1974).Google Scholar
7. Geramita, A. V. and Sebbery, J., Orthogonal designs (Marrel Dekker, New York, 1979).Google Scholar
8. Shapire, B., Spaces of similarities IV: (S, t) families, Pac. J. Math. 69 (1977).Google Scholar
9. Wolfe, W., Amicable orthogonal designs—existence, Can. J. Math. 28 (1976).Google Scholar