Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Patras, Frédéric
Reutenauer, Christophe
and
Schocker, Manfred
2005.
On the Garsia Lie Idempotent.
Canadian Mathematical Bulletin,
Vol. 48,
Issue. 3,
p.
445.
Schocker, Manfred
2006.
The module structure of the Solomon–Tits algebra of the symmetric group.
Journal of Algebra,
Vol. 301,
Issue. 2,
p.
554.
Mafra, Carlos R.
and
Schlotterer, Oliver
2016.
Berends-Giele recursions and the BCJ duality in superspace and components.
Journal of High Energy Physics,
Vol. 2016,
Issue. 3,
Mafra, Carlos R.
2016.
Berends-Giele recursion for double-color-ordered amplitudes.
Journal of High Energy Physics,
Vol. 2016,
Issue. 7,
Mafra, Carlos R.
and
Schlotterer, Oliver
2017.
Non-abelian Z-theory: Berends-Giele recursion for the α ′-expansion of disk integrals.
Journal of High Energy Physics,
Vol. 2017,
Issue. 1,
Mafra, Carlos R.
and
Schlotterer, Oliver
2019.
Towards the n-point one-loop superstring amplitude. Part I. Pure spinors and superfield kinematics.
Journal of High Energy Physics,
Vol. 2019,
Issue. 8,
Gerken, Jan E.
Kleinschmidt, Axel
and
Schlotterer, Oliver
2020.
All-order differential equations for one-loop closed-string integrals and modular graph forms.
Journal of High Energy Physics,
Vol. 2020,
Issue. 1,
Broedel, Johannes
Kaderli, André
and
Schlotterer, Oliver
2020.
Two dialects for KZB equations: generating one-loop open-string integrals.
Journal of High Energy Physics,
Vol. 2020,
Issue. 12,
Mafra, Carlos R.
and
Schlotterer, Oliver
2020.
One-loop open-string integrals from differential equations: all-order α′-expansions at n points.
Journal of High Energy Physics,
Vol. 2020,
Issue. 3,
Mafra, Carlos R.
2022.
KK-like relations of α′ corrections to disk amplitudes.
Journal of High Energy Physics,
Vol. 2022,
Issue. 3,
Mafra, Carlos R.
and
Schlotterer, Oliver
2023.
Tree-level amplitudes from the pure spinor superstring.
Physics Reports,
Vol. 1020,
Issue. ,
p.
1.
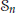 ${{\mathcal{S}}_{n}}$ consists of all permutations in
${{\mathcal{S}}_{n}}$ consists of all permutations in 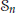 ${{\mathcal{S}}_{n}}$ with a given Schensted
${{\mathcal{S}}_{n}}$ with a given Schensted 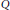 $Q$-symbol, and may be described in terms of local relations introduced by Knuth. Any Lie element in the group algebra of
$Q$-symbol, and may be described in terms of local relations introduced by Knuth. Any Lie element in the group algebra of 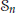 ${{\mathcal{S}}_{n}}$ which is constant on coplactic classes is already constant on descent classes. As a consequence, the intersection of the Lie convolution algebra introduced by Patras and Reutenauer and the coplactic algebra introduced by Poirier and Reutenauer is the direct sum of all Solomon descent algebras.
${{\mathcal{S}}_{n}}$ which is constant on coplactic classes is already constant on descent classes. As a consequence, the intersection of the Lie convolution algebra introduced by Patras and Reutenauer and the coplactic algebra introduced by Poirier and Reutenauer is the direct sum of all Solomon descent algebras.

