Hostname: page-component-cd9895bd7-dzt6s Total loading time: 0 Render date: 2024-12-18T13:12:21.353Z Has data issue: false hasContentIssue false
  • English
  • Français

L-Functions for GSp(2) × GL(2): Archimedean Theory and Applications

Published online by Cambridge University Press:  20 November 2018

Tomonori Moriyama
Tomonori Moriyama*
Affiliation:
Department of Mathematics, Osaka University, Machikaneyama 1-1, Toyonaka, Osaka, 560-0043, Japan, [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 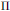$\Pi$ be a generic cuspidal automorphic representation of 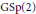$\text{GSp}\left( 2 \right)$ defined over a totally real algebraic number field 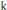$\text{k}$ whose archimedean type is either a (limit of) large discrete series representation or a certain principal series representation. Through explicit computation of archimedean local zeta integrals, we prove the functional equation of tensor product $L$-functions 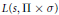$L\left( s,\Pi \times \sigma \right)$ for an arbitrary cuspidal automorphic representation 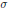$\sigma $ of 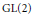$\text{GL}\left( 2 \right)$. We also give an application to the spinor $L$-function of 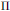$\Pi$.

Keywords

11F7011F4111F46
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 61 , Issue 2 , 01 April 2009 , pp. 395 - 426
Copyright
Copyright © Canadian Mathematical Society 2009

References

[A-S-1] Asgari, M. and Shahidi, F., Generic transfer for general spin groups. Duke Math. J. 132(2006), 137–190.Google Scholar
[A-S-2] Asgari, M. and Shahidi, F., Generic transfer from GSp(4) to GL(4. Compos. Math. 142(2006), 541–550.Google Scholar
[A-G-R] Ash, A., Ginzburg, D., and Rallis, S., Vanishing periods of cusp forms over modular symbols , Math. Ann. 296(1993), no. 4, 709–723.Google Scholar
[Ba-M] Barbasch, D. and Moy, A., Whittaker models with an Iwahori fixed vector. In: Representation theory and analysis on homogeneous spaces, Contemp. Math. 177, American Mathematical Soiety, Providence, RI, 1994, pp. 101–105.Google Scholar
[Bo-He] Böcherer, S. and Heim, B., L-functions on GSp2 × Gl2 of mixed weights. Math. Z. 235(2000), no. 1, 11–51.Google Scholar
[Bo] Borel, A., Automorphic L-functions. In: Automorphic forms, representations and L -functions, Proc. Sympos. Pure Math. 33, American Mathematical Society, Providence, RI, 1979, pp. 27–61.Google Scholar
[Bu] Bump, D., The Rankin-Selberg method: a survey. In: Number theory, trace formulas and discrete groups, Academic Press, Boston, MA, 1989, pp. 49–109.Google Scholar
[C-S] Casselman, W. and Shalika, J., The unramified principal series of p-adic groups. II. The Whittaker function. Compositio Math. 41(1980), no. 2, 207–231.Google Scholar
[Co] Cogdell, J. W., Lectures on L-functions, converse theorems, and functoriality for GLn. In: Lectures on automorphic L -functions, Fields Inst. Monogr.20, American Mathematical Society, Providence, RI, 2004, pp. 1–96.Google Scholar
[Fu] Furusawa, M., On L-functions for GSp(4) × GL(2) and their special values. J. Reine Angew. Math. 438(1993), 187–218.Google Scholar
[G-PS-R] Gelbart, S., Piatetski-Shapiro, I., and Rallis, S., Explicit Constructions of Automorphic L-functions. Lecture Notes in Mathematics 1254, Springer-Verlag, Berlin, 1987.Google Scholar
[G-Sh] Gelbart, S. and Shahidi, F., Analytic properties of automorphic L-functions. Perspectives in Mathematics 6, Academic Press, Inc., Boston, MA, 1988.Google Scholar
[Ha] Harris, M., Occult period invariants and critical values of the degree four L-function of GSp4. In: Contributions to automorphic forms, geometry, and number theory, Johns Hopkins University Press, Baltimore, MD, 2004, 331–354.Google Scholar
[He] Heim, B., Pullbacks of Eisenstein series, Hecke-Jacobi theory and automorphic L-functions. In: Automorphic forms, automorphic representations, and arithmetic, Proc. Sympos. Pure Math. 66, American Mathematical Society, Providence, RI, 1999, pp. 201–238.Google Scholar
[J-1] Jacquet, H., Fonctions de Whittaker associées aux groupes de Chevalley. Bull. Soc. Math. France 95(1967), 243–309.Google Scholar
[J-2] Jacquet, H., Automorphic forms on GL (2). II. Lecture Notes in Mathematics 278, Springer-Verlag, Berlin-New York, 1972.Google Scholar
[J-S] Jacquet, H. and Shalika, J. A., On Euler products and the classification of automorphic representations. I. Amer. J. Math. 103(1981), no. 3, 499–558.Google Scholar
[Ki] Kim, H., Automorphic L-functions. In: Lectures on automorphic L -functions, Fields Inst. Monogr. 20, American Mathematical Society, Providence, RI, 2004, pp. 97–201.Google Scholar
[Li] J.-S. Li, Some results on the unramified principal series of p-adic groups. Math. Ann. 292(1992), no. 4, 747–761.Google Scholar
[Mi-O-1] Miyazaki, T. and Oda, T., Principal series Whittaker functions on Sp(2; R). II. Tohoku Math. J. (2) 50(1998), no. 2, 243–260.Google Scholar
[Mi-O-2] Miyazaki, T. and Oda, T., Errata: Principal series Whittaker functions on Sp(2; R). II. Tohoku Math. J. (2) 54(2002), no. 1, 161–162.Google Scholar
[Mo-1] Moriyama, T., Spherical functions with respect to the semisimple symmetric pair (Sp (2, R), SL (2, R) × SL (2, R). J. Math. Sci. Univ. Tokyo 6(1999), no. 1, 127–179.Google Scholar
[Mo-2] Moriyama, T., A remark on Whittaker functions on Sp(2, R. J. Math. Sci. Univ. Tokyo 9(2002), no. 4, 627–635.Google Scholar
[Mo-3] Moriyama, T., Entireness of the spinor L-functions for certain generic cusp forms on GSp (2. Amer. J. Math. 126(2004), no. 4, 899–920.Google Scholar
[Ni] Niwa, S., Commutation relations of differential operators and Whittaker functions on Sp 2(R. Proc. Japan Acad. Ser. A. Math. Sci. 71(1995), no. 8, 189–191.Google Scholar
[No-1] Novodvorsky, M. E., Fonction J pour des groupes orthogonaux. C. R. Acad. Sci. Paris Sér. A-B 280(1975), A1421–A1422.Google Scholar
[No-2] Novodvorsky, M. E., Automorphic L-functions for symplectic group GSp (4). In: Automorphic forms, representations and L -functions, Proc. Sympos. Pure Math. 33, American Mathematic Society, Providence, RI, 1979, 87–95.Google Scholar
[O] Oda, T., An explicit integral representation of Whittaker functions on Sp(2; R) for large discrete series representations. Tohoku Math. J. 46(1994), no. 2, 261–279.Google Scholar
[PS] Piatetski-Shapiro, I. I., L-functions for GSp4, Olga Taussky-Todd: in memoriam. Pacific J. Math. 1997, Special Issue, 259–275.Google Scholar
[PS-S] Piatetski-Shapiro, I. I. and Soudry, D., L and ϵ functions for GSp(4) × GL(2. Proc. Nat. Acad. Sci. U. S. A. 81(1984), no. 12, Phys. Sci., 3924–3927.Google Scholar
[Re] Reeder, M., p-adic Whittaker functions and vector bundles on flag manifolds. Compositio Math. 85(1993), no. 1, 9–36.Google Scholar
[Ro] Rodier, F., Whittaker models for admissible representations of reductive p-adic split groups. In: Harmonic analysis on homogeneous spaces, Proc. Sympos. Pure Math. 26, American Mathematical Society, Providence, RI, 1973, 425–430.Google Scholar
[Sha] Shalika, J. A., The multiplicity one theorem for GLn. Ann. of Math. 100(1974), 171–193.Google Scholar
[Shm] Shimura, G., The special value of the zeta functions associated with cusp forms. Comm. Pure Appl. Math. 29(1976), no. 6, 783–804.Google Scholar
[So-1] Soudry, D., The L and γ factors for generic representations of GSp (4, k ) × GL (2, k ) over a local non-Archimedean field k. Duke Math. J. 51(1984), no. 2, 355–394.Google Scholar
[So-2] Soudry, D., On the Archimedean theory of Rankin-Selberg convolutions for SO2l +1 × GLn. Ann. Sci. École Norm. Sup. 28(1995), no. 2, 161–224.Google Scholar
[Wa] Wallach, N. R., Asymptotic expansions of generalized matrix entries of representations of real reductive groups. In: Lie group representations, I., Lecture Notes in Math. 1024, Springer, Berlin, 1983, pp. 287–369.Google Scholar
[W-W] Whittaker, E. T. and Watson, G. N., A course of modern analysis. An introduction to the general theory of infinite processes and of analytic functions; with an account of the principla transcendental functions. Reprint of the fourth (1927) edition, Cambridge University Press, Cambrigde, 1996.Google Scholar