Les θ-régulateurs locaux d'un nombre algébrique : Conjectures p-adiques

Abstract

Let 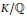$K/\mathbb{Q}$ be Galois and let 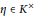$\eta \,\in \,{{K}^{\times }}$ be such that 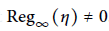$\text{Re}{{\text{g}}_{\infty }}\left( \eta \right)\,\ne \,0$. We define the local 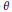$\theta $-regulator 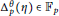$\Delta _{p}^{\theta }\left( \eta \right)\,\in \,{{\mathbb{F}}_{p}}$ for the 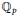${{\mathbb{Q}}_{p}}$-irreducible characters 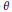$\theta $ of 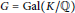$G=\,\text{Gal}\left( K/\mathbb{Q} \right)$. Let 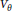${{V}_{\theta }}$ be the 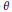$\theta $-irreducible representation. A linear representation 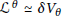${{\mathfrak{L}}^{\theta }}\,\simeq \,\delta \,{{V}_{\theta }}$ is associated with 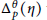$\Delta _{p}^{\theta }\left( \eta \right)$ whose nullity is equivalent to 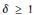$\delta \,\ge \,1$. Each 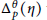$\Delta _{p}^{\theta }\left( \eta \right)$ yields 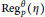$\text{R}eg_{p}^{\theta }\left( \eta \right)$ modulo 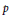$p$ in the factorization 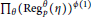${{\Pi }_{\theta }}{{\left( \text{Reg}_{p}^{\theta }\left( \eta \right) \right)}^{\phi \left( 1 \right)}}$ of 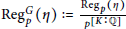$\text{Reg}_{p}^{G}\,\left( \eta \right)\,:=\frac{\text{Re}{{\text{g}}_{p}}\left( \eta \right)}{_{p}[K\,:\,\mathbb{Q}]}$ (normalized 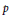$p$-adic regulator). From Prob 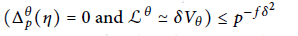$\left( \Delta _{p}^{\theta }\left( \eta \right)=0\,\text{and}\,{{\mathfrak{L}}^{\theta }}\simeq \delta {{V}_{\theta }} \right)\,\le {{p}^{-f{{\delta }^{2}}}}$ (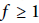$f\,\ge \,1$ is a residue degree) and the Borel-Cantelli heuristic, we conjecture that for 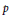$p$ large enough, 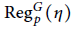$\text{Reg}_{p}^{G}\left( \eta \right)$ is a 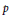$p$-adic unit or 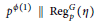${{p}^{\phi \left( 1 \right)}}\,||\,\text{Reg}_{p}^{G}\left( \eta \right)$ (a single 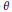$\theta $ with 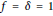$f\,=\,\delta \,=\,1$); this obstruction may be led assuming the existence of a binomial probability law confirmed through numerical studies (groups 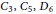${{C}_{3,}}\,{{C}_{5}},\,{{D}_{6}}$) is conjecture would imply that for all 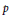$p$ large enough, Fermat quotients, normalized 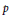$p$-adic regulators are 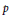$p$-adic units and that number fields are 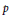$p$-rational.We recall some deep cohomological results that may strengthen such conjectures.