Article contents
Lattices With a Given Abstract Group of Automorphisms
Published online by Cambridge University Press: 20 November 2018
Extract
The problem of finding a lattice with a given abstract group of automorphisms has been solved by Garrett Birkhoff who proved that for any group of order g there exists a distributive lattice with at most 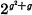 elements. That this number can be somewhat reduced by modifications of Birkhoff's original procedure has already been shown by the author; it turns out, however, that it remains rather high for finite groups of relatively low order.
elements. That this number can be somewhat reduced by modifications of Birkhoff's original procedure has already been shown by the author; it turns out, however, that it remains rather high for finite groups of relatively low order.
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 1950
References
1 For the definition of lattice and other basic notions of lattice theory, see Garrett Birkhoff's Lattice Theory (1st ed., New York, 1940).
2 Birkhoff, Garrett, Sobre los grupos de automorfismos. Revista de la Union Matematica Argentina, vol. 11 (1946), pp. 155–157.Google Scholar
3 Frucht, R., Sobre la construction de sistemas parcialmente ordenados con grupo de automorfismos dado. Revista de la Union Matematica Argentina, vol. 13 (1948), pp. 12–18. See also: On the construction of partially ordered systems with a given group of automorphisms. Amer. J. Math., vol. 72 (1950), pp. 195–199.Google Scholar
4 In other words, S is the “cell-space” P(G) of G (see Lattice Theory, 1st ed., p. 15) to which an 0 has been added in order to obtain a lattice.
5 The “Hasse diagram” of this lattice may be obtained from the right-hand half of Fig 2 p. 15, of Lattice Theory by adding an 0 and joining it with B1, B2, B3 and B4.
6 Lattice Theory, 1st ed., p. 34, Corollary 3 to Theorem 3.1.
7 By “X covers A” it is meant that X > A, while no Z of 5 satisfies X > Z > A.
8 Frucht, R., Graphs of degree 3 with a given abstract group. Can. J. Math., vol. 1 (1949), pp. 365–378.CrossRefGoogle Scholar
- 28
- Cited by


