No CrossRef data available.
Article contents
Large Deviations for Gaussian Stochastic Processes with Sample Paths in Orlicz Spaces
Published online by Cambridge University Press: 20 November 2018
Extract
Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.
Let X be a complete, separable metric space, and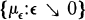 
a family of probability measures on the Borel subsets of X. We say that 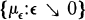obeys the large deviation principle (LDP) with a rate function I( · ) if there exists a function I( · ) from X into [0, ∞] satisfying:
(i) 0 ≦ I(x) ≦ ∞ for all x ∊ X,
(ii) I( · ) is lower semicontinuous,
(iii) for each 1 < ∞ the set {x:I(x) ≦ 1} is compact set in X,
(iv) for each closed set C ⊂ X
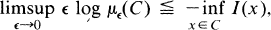
(v) for each open set U ⊂ X
It is easy to see that if A is a Borel set such that
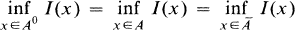
then
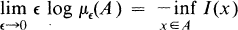
where A0 and Ā are respectively the interior and the closure of the Borel set A.
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 1988
References
1.
Bahadur, R. R. and Zabell, S. L., Large deviations of the sample mean in general vector spaces, Ann. Probab.
7 (1979), 587–621.Google Scholar
2.
Byczkowski, T., Gaussian measures on Lp spaces, 0 < p < ∞, Studia Math. 59 (1977), 249–261.Google Scholar
3.
Byczkowski, T., Norm convergent expansion for Lϕ-valued Gaussian random elements, Studia Math.
64 (1979), 87–95.Google Scholar
4.
Byczkowski, T. and Zak, T., On the integrability of Gaussian random vectors, Lecture Notes in Math.
828 (Springer, New York, 1979), 21–30.Google Scholar
5.
Cramer, H., Sur un nouveau théorème-limite de la théorie des probabilités, Actualités Sci. Indust.
736 (1938), 5–23.Google Scholar
6.
Donsker, M. D. and Varadhan, S. R. S., Asymptotic evaluation for certain Markov processes expectations for large-time III, Comm. Pure Appl. Math.
29 (1976), 389–461.Google Scholar
7.
Kallianapur, G. and Oodaira, H., Freidlin-Wentzell type estimates for abstract Wiener spaces, Sankhya
40, Series A (1978), 116–137.Google Scholar
8.
Lawniczak, A. T., Gaussian measures on Orlicz spaces and abstract Wiener spaces, Lecture Notes in Math.
939 (Springer, New York, (1982), 81–97.Google Scholar
9.
Lawniczak, A. T., High level occupation times for Gaussian stochastic processes with sample paths in Orlicz spaces, Can. J. Math.
39 (1987), 239–256.Google Scholar
10.
Marlow, N., High level occupation times for continuous Gaussian processes, Ann. Probab.
3 (1973), 388–397.Google Scholar
12.
Stroock, D. W., An introduction to the theory of large deviations (Springer-Verlag, New York, (1984).CrossRefGoogle Scholar
You have
Access