Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Gelbart, Stephen
and
Shahidi, Freydoon
2000.
Boundedness of automorphic 𝐿–functions in vertical strips.
Journal of the American Mathematical Society,
Vol. 14,
Issue. 1,
p.
79.
Kim, Henry H.
and
Shahidi, Freydoon
2000.
Holomorphy of Rankin tripleL-functions; special values and root numbers for symmetric cubeL-functions.
Israel Journal of Mathematics,
Vol. 120,
Issue. 2,
p.
449.
Kim, Henry H.
2000.
Langlands-shahidi method and poles of automorphicL-functions II.
Israel Journal of Mathematics,
Vol. 117,
Issue. 1,
p.
261.
Kim, Henry H.
and
Shahidi, Freydoon
2002.
Cuspidality of symmetric powers with applications.
Duke Mathematical Journal,
Vol. 112,
Issue. 1,
Kim, Henry
2002.
Functoriality for the exterior square of 𝐺𝐿₄ and the symmetric fourth of 𝐺𝐿₂.
Journal of the American Mathematical Society,
Vol. 16,
Issue. 1,
p.
139.
Gelbart, Stephen
and
Miller, Stephen
2003.
Riemann’s zeta function and beyond.
Bulletin of the American Mathematical Society,
Vol. 41,
Issue. 1,
p.
59.
Asgari, Mahdi
and
Shahidi, Freydoon
2006.
Generic transfer for general spin groups.
Duke Mathematical Journal,
Vol. 132,
Issue. 1,
Shahidi, Freydoon
2008.
Representation Theory and Automorphic Forms.
Vol. 255,
Issue. ,
p.
151.
Kim, Henry H.
2008.
Langlands–Shahidi method and poles of automorphic L-functions III: Exceptional groups.
Journal of Number Theory,
Vol. 128,
Issue. 2,
p.
354.
Miller, Stephen D.
and
Schmid, Wilfried
2008.
Representation Theory and Automorphic Forms.
Vol. 255,
Issue. ,
p.
111.
Anandavardhanan, U. K.
2008.
Root Numbers of Asai L-Functions.
International Mathematics Research Notices,
Vol. 2008,
Issue. ,
Lomeli, L. A.
2009.
Functoriality for the Classical Groups over Function Fields.
International Mathematics Research Notices,
Grbac, Neven
2009.
On the residual spectrum of Hermitian quaternionic inner form of SO_8.
Glasnik Matematicki,
Vol. 44,
Issue. 1,
p.
11.
Blomer, Valentin
and
Brumley, Farrell
2011.
On the Ramanujan conjecture over number fields.
Annals of Mathematics,
Vol. 174,
Issue. 1,
p.
581.
Ginzburg, David
Jiang, Dihua
and
Soudry, David
2012.
On correspondences between certain automorphic forms on $$Sp_{4n} (\mathbb{A})$$ and $$\widetilde{Sp}_{2n} (\mathbb{A})$$.
Israel Journal of Mathematics,
Vol. 192,
Issue. 2,
p.
951.
Blomer, Valentin
and
Brumley, Farrell
2013.
The role of the Ramanujan conjecture in analytic number theory.
Bulletin of the American Mathematical Society,
Vol. 50,
Issue. 2,
p.
267.
Soudry, David
2017.
The unramified computation of Rankin–Selberg integrals expressed in terms of Bessel models for split orthogonal groups: Part I.
Israel Journal of Mathematics,
Vol. 222,
Issue. 2,
p.
711.
Ishii, Taku
2018.
Archimedean zeta integrals for the exterior square L-functions on GL.
Journal of Number Theory,
Vol. 186,
Issue. ,
p.
304.
Lomelí, Luis Alberto
2019.
Rationality and holomorphy of Langlands–Shahidi L-functions over function fields.
Mathematische Zeitschrift,
Vol. 291,
Issue. 1-2,
p.
711.
Jiang, Yujiao
and
Lü, Guangshi
2019.
Quantitative non-vanishing results on L-functions.
The Quarterly Journal of Mathematics,
Vol. 70,
Issue. 3,
p.
813.
 $L$-functions on the whole complex plane which appear in constant terms of the Eisenstein series. They include the exterior square
$L$-functions on the whole complex plane which appear in constant terms of the Eisenstein series. They include the exterior square  $L$-functions of
$L$-functions of 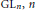 $\text{G}{{\text{L}}_{\text{n}}},\,n$ odd, the Rankin-Selberg
$\text{G}{{\text{L}}_{\text{n}}},\,n$ odd, the Rankin-Selberg  $L$-functions of
$L$-functions of 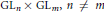 $\text{G}{{\text{L}}_{n}}\times \,\text{G}{{\text{L}}_{m}},\,n\,\ne \,m$, and
$\text{G}{{\text{L}}_{n}}\times \,\text{G}{{\text{L}}_{m}},\,n\,\ne \,m$, and  $L$-functions
$L$-functions 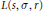 $L\left( s,\,\sigma ,\,r \right)$, where
$L\left( s,\,\sigma ,\,r \right)$, where  $\sigma $ is a generic cuspidal representation of
$\sigma $ is a generic cuspidal representation of 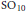 $\text{S}{{\text{O}}_{10}}$ and
$\text{S}{{\text{O}}_{10}}$ and  $r$ is the half-spin representation of GSpin
$r$ is the half-spin representation of GSpin 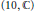 $\left( 10,\,\mathbb{C} \right)$. The main part is proving the holomorphy and non-vanishing of the local normalized intertwining operators by reducing them to natural conjectures in harmonic analysis, such as standard module conjecture.
$\left( 10,\,\mathbb{C} \right)$. The main part is proving the holomorphy and non-vanishing of the local normalized intertwining operators by reducing them to natural conjectures in harmonic analysis, such as standard module conjecture.

