Hostname: page-component-586b7cd67f-l7hp2 Total loading time: 0 Render date: 2024-11-24T04:13:42.792Z Has data issue: false hasContentIssue false
  • English
  • Français

Klein's Oscillation Theorem for Periodic Boundary Conditions

Published online by Cambridge University Press:  20 November 2018

A. Howe
A. Howe*
Affiliation:
Australian National University, Canberra, A.C.T.
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Multiparameter eigenvalue problems for systems of linear differential equations with homogeneous boundary conditions have been considered by Ince [4] and Richardson [5, 6], and more recently Faierman [3] has considered their completeness and expansion theorems. A survey of eigenvalue problems with several parameters, in mathematics, is given by Atkinson [1].

We consider the two differential equations:

1a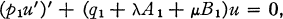

1b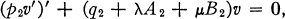

where p1’(x), q1(x), A1(x), B1(x) and p2’(y), q2(y), A2(y), B2(y) are continuous for x ∈ [a1, b1] and y ∈ [a2, b2] respectively, and p1 (x) > 0(x ∈ [a1, b1]), p2(y) > 0 (y ∈ [a2, b2]), p1(a1) = p1(b1), p2(a2) = p2(b2). The differential equations (1) will be subjected to the periodic boundary conditions.

2a

2b

Let us consider a single differential equation

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 23 , Issue 4 , August 1971 , pp. 699 - 703
Copyright
Copyright © Canadian Mathematical Society 1971

References

1. Atkinson, F. V., Multiparameter spectral theory, Bull. Amer. Math. Soc. 74 (1968), 1–27.Google Scholar
2. Coddington, E. A. and Levinson, N., Theory of ordinary differential equations (McGraw-Hill, New York, 1955).Google Scholar
3. Faierman, M., The completeness and expansion theorems associated with the multiparameter eigenvalue problem in ordinary differential equations, J. Differential Equations 5 (1969), 197–213.Google Scholar
4. Ince, E. L., Ordinary differential equations (Dover, New York, 1956).Google Scholar
5. Richardson, R. G. D., Theorems of oscillation for two linear differential equations of the second order with two parameters, Trans. Amer. Math. Soc. 18 (1912), 22–34.Google Scholar
6. Richardson, R. G. D., Über die notwendigen und hinreichenden Bedingungen fur das Bestehen eines Kleinschen Oszillations Theorems, Math. Ann. 73 (1913), 289–304.Google Scholar