Hostname: page-component-78c5997874-v9fdk Total loading time: 0 Render date: 2024-11-14T07:25:32.144Z Has data issue: false hasContentIssue false
  • English
  • Français

Isoresonant Complex-valued Potentials and Symmetries

Published online by Cambridge University Press:  20 November 2018

Aymeric Autin
Aymeric Autin*
Affiliation:
11 rue Hélène Boucher, 85400 Luçon, France email: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 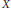$X$ be a connected Riemannian manifold such that the resolvent of the free Laplacian 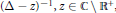${{(\Delta -z)}^{-1}},\,z\,\in \,\mathbb{C}\backslash {{\mathbb{R}}^{+}}$, has a meromorphic continuation through 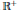${{\mathbb{R}}^{+}}$. The poles of this continuation are called resonances. When 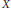$X$ has some symmetries, we construct complex-valued potentials, 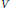$V$, such that the resolvent of 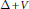$\Delta \,+\,V$, which has also a meromorphic continuation, has the same resonances with multiplicities as the free Laplacian.

Keywords

31C1258J50
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 63 , Issue 4 , 01 August 2011 , pp. 721 - 754
Copyright
Copyright © Canadian Mathematical Society 2011

References

[Agm98] Agmon, S., A perturbation theory of resonances. Commun. Pure Appl. Math. 51(1998), 1255–1309. doi:10.1002/(SICI)1097-0312(199811/12)51:11/12h1255::AID-CPA2i3.0.CO;2-OGoogle Scholar
[Aut08] Autin, A., Potentiels isorésonants et symétries. Thèse, Université de Nantes, 2008. http://tel.archives-ouvertes.fr/tel-00336843Google Scholar
[BGM71] Berger, M., Gauduchon, P. and Mazet, E., Le spectre d’une variété riemannienne. Lecture Notes in Mathematics 194, Springer-Verlag, Berlin, 1971.Google Scholar
[CdV79] Colin de Verdière, Y., Spectre conjoint d’opérateurs pseudo-différentiels qui commutent. I. Le cas non intégrable. Duke Math. J. 46(1979), 169–182. doi:10.1215/S0012-7094-79-04608-8Google Scholar
[Chr99] Christiansen, T., Some lower bounds on the number of resonances in Euclidean scattering. Math. Res. Lett. 6(1999), 203–211.Google Scholar
[Chr06] Christiansen, T., Schrödinger operators with complex-valued potentials and no resonances. Duke Math. J. 133(2006), 313–323. doi:10.1215/S0012-7094-06-13324-0Google Scholar
[Chr08] Christiansen, T., Isophasal, isopolar, and isospectral schrödinger operators and elementary complex analysis. Amer. J. Math. 130(2008), 49–58. doi:10.1353/ajm.2008.0002Google Scholar
[FH91] Fulton, W. and Harris, J., Representation theory. Graduate Texts in Mathematics 129, Springer-Verlag, New York, 1991.Google Scholar
[GK71] Gohberg, I. C. and Krejn, M. G., Introduction à la théorie des opérateurs linéaires non auto-adjoints dans un espace hilbertien. Dunod, Paris, 1971.Google Scholar
[GU83] Guillemin, V. and Uribe, A., Spectral properties of a certain class of complex potentials. Trans. Amer. Math. Soc. 279(1983), 759–771. doi:10.1090/S0002-9947-1983-0709582-8Google Scholar
[Gui05] Guillarmou, C., Meromorphic properties of the resolvent on asymptotically hyperbolic manifolds. Duke Math. J. 129(2005), 1–37. doi:10.1215/S0012-7094-04-12911-2Google Scholar
[GZ95a] Guillopé, L. and Zworski, M., Polynomial bounds on the number of resonances for some complete spaces of constant negative curvature near infinity. Asymptotic Anal. 11(1995), 1–22.Google Scholar
[GZ95b] Guillopé, L. and Zworski, M., Upper bounds on the number of resonances for non-compact Riemann surfaces. J. Funct. Anal. 129(1995), 364–389. doi:10.1006/jfan.1995.1055Google Scholar
[HP09] Hilgert, J. and Pasquale, A., Resonances and residue operators for symmetric spaces of rank one. J. Math. Pures Appl. 91(2009), 495–507. doi:10.1016/j.matpur.2009.01.009Google Scholar
[Kat66] Kato, T., Perturbation theory for linear operators. Die Grundlehren der mathematischen Wissenschaften, Band 132, Springer-Verlag New York, Inc., New York, 1966.Google Scholar
[Mel93] Melrose, R. B., The Atiyah–Patodi–Singer index theorem. Research Notes in Mathematics 4, Peters, A. K., Ltd.,Wellesley, MA, 1993.Google Scholar
[Mel95] Melrose, R. B., Geometric scattering theory. In: Stanford Lectures, Cambridge University Press, Cambridge, 1995.Google Scholar
[MM87] Mazzeo, R. R. and Melrose, R. B., Meromorphic extension of the resolvent on complete spaces with asymptotically constant negative curvature. J. Funct. Anal. 75(1987), 260–310. doi:10.1016/0022-1236(87)90097-8Google Scholar
[SB99] Sá Barreto, A., Lower bounds for the number of resonances in even-dimensional potential scattering. J. Funct. Anal. 169(1999), 314–323. doi:10.1006/jfan.1999.3438Google Scholar
[SBZ95] Sá Barreto, A. and Zworski, M., Existence of resonances in three dimensions. Comm. Math. Phys. 173(1995), 401–415. doi:10.1007/BF02101240Google Scholar
[Sim96] Simon, B., Representations of finite and compact groups. Graduate Studies in Mathematics 10, Amer. Math. Soc., Providence, RI, 1996.Google Scholar
[SZ91] Sjöstr, J. and and Zworski, M., Complex scaling and the distribution of scattering poles. J. Amer. Math. Soc. 4(1991), 729–769.Google Scholar
[WZ00] Wunsch, J. and Zworski, M., Distribution of resonances for asymptotically Euclidean manifolds. J. Differential Geom. 55(2000), 43–82.Google Scholar
[Yaf92] Yafaev, D. R., Mathematical scattering theory. Transl. Math. Monogr. 105, American Mathematical Society, Providence, RI, 1992.Google Scholar