Article contents
Isomorphic Structure of Cesàro and Tandori Spaces
Published online by Cambridge University Press: 09 January 2019
Abstract
We investigate the isomorphic structure of the Cesàro spaces and their duals, the Tandori spaces. The main result states that the Cesàro function space 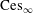 $\text{Ces}_{\infty }$ and its sequence counterpart
$\text{Ces}_{\infty }$ and its sequence counterpart 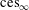 $\text{ces}_{\infty }$ are isomorphic. This is rather surprising since
$\text{ces}_{\infty }$ are isomorphic. This is rather surprising since 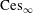 $\text{Ces}_{\infty }$ (like Talagrand’s example) has no natural lattice predual. We prove that
$\text{Ces}_{\infty }$ (like Talagrand’s example) has no natural lattice predual. We prove that 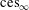 $\text{ces}_{\infty }$ is not isomorphic to
$\text{ces}_{\infty }$ is not isomorphic to 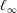 $\ell _{\infty }$ nor is
$\ell _{\infty }$ nor is 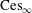 $\text{Ces}_{\infty }$ isomorphic to the Tandori space
$\text{Ces}_{\infty }$ isomorphic to the Tandori space 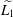 $\widetilde{L_{1}}$ with the norm
$\widetilde{L_{1}}$ with the norm 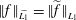 $\Vert f\Vert _{\widetilde{L_{1}}}=\Vert \widetilde{f}\Vert _{L_{1}}$, where
$\Vert f\Vert _{\widetilde{L_{1}}}=\Vert \widetilde{f}\Vert _{L_{1}}$, where 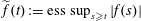 $\widetilde{f}(t):=\text{ess}\,\sup _{s\geqslant t}|f(s)|$. Our investigation also involves an examination of the Schur and Dunford–Pettis properties of Cesàro and Tandori spaces. In particular, using results of Bourgain we show that a wide class of Cesàro–Marcinkiewicz and Cesàro–Lorentz spaces have the latter property.
$\widetilde{f}(t):=\text{ess}\,\sup _{s\geqslant t}|f(s)|$. Our investigation also involves an examination of the Schur and Dunford–Pettis properties of Cesàro and Tandori spaces. In particular, using results of Bourgain we show that a wide class of Cesàro–Marcinkiewicz and Cesàro–Lorentz spaces have the latter property.
Keywords
MSC classification
- Type
- Article
- Information
- Copyright
- © Canadian Mathematical Society 2018
Footnotes
Author S. V. A. was partially supported by the Ministry of Education and Science of the Russian Federation (project 1.470.2016/1.4) and author K. L. was partially supported by the grant 04/43/DSPB/0086 from the Polish Ministry of Science and Higher Education.
References
- 3
- Cited by


