Hostname: page-component-745bb68f8f-hvd4g Total loading time: 0 Render date: 2025-01-23T23:15:39.836Z Has data issue: false hasContentIssue false
  • English
  • Français

Isometric Immersions of almost Hermitian Manifolds

Published online by Cambridge University Press:  20 November 2018

Alfred Gray
Alfred Gray*
Affiliation:
University of California, Berkeley, California University of Maryland, College Park, Maryland
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The Lefschetz theorem on hyperplane sections, as proved by Andreotti and Frankel (1), depends upon the following result.

THEOREM. If M is a non-singular affine algebraic variety of real dimension 2k of complex n-space, then

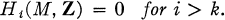
This theorem, which is interesting in itself, has been strengthened by Milnor (7), who showed that M has the homotopy type of a k-dimensional CW-complex.

In this paper we generalize the above theorem in two directions. First, we replace complex n-space by some other complete simply connected Riemannian manifold 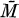which either has non-positive curvature or is a compact symmetric space. Secondly, we allow M and 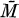to be quasi-Kâhlerian (see below) instead of Kählerian.

We first introduce some notation. Let M and 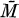be C∞ Riemannian manifolds with M isometrically immersed in 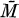. Denote by 〈, 〉 the metric tensor of either M or .

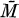Type
Research Article
Information
Canadian Journal of Mathematics , Volume 21 , 1969 , pp. 456 - 459
Copyright
Copyright © Canadian Mathematical Society 1969

References

1. Andreotti, A. and Frankel, T., The Lefschetz theorem on hyperplane sections, Ann. of Math. (2) 69 (1959), 713–717.Google Scholar
2. Bishop, R. L. and Crittenden, R. J., Geometry of manifolds (Academic Press, New York, 1964).Google Scholar
3. Gray, A., Minimal varieties and almost Hermitian submanifolds, Michigan Math. J. 12 (1965), 273–287.Google Scholar
4. Gray, A., Vector cross products on manifolds, Trans. Amer. Math. Soc. (to appear).Google Scholar
5. Gray, A., Almost complex submanifolds of the six sphere, Proc. Amer. Math. Soc. 20 (1969), 277–279.Google Scholar
6. Gray, A., Isometric immersions in symmetric spaces, J. Differential Geometry (to appear).Google Scholar
7. Hermann, R., Focal points of closed submanifolds of Riemannian spaces, Nederl. Akad. Wetensch. Proc. Ser. A 66 (1963), 619–628.Google Scholar
8. Milnor, J., Lectures on Morse theory, Ann. Math. Studies, No. 54 (Princeton University Press, Princeton, N.J., 1963).Google Scholar
9. Sternberg, S., Lectures on differential geometry (Prentice-Hall, Englewood Cliffs, N.J., 1964).Google Scholar
10. Wolf, J. A. and Gray, A., Homogeneous spaces defined by Lie group automorphisms. J. Differential Geometry 2 (1968), 77–159 Google Scholar