Article contents
Irreducible Representations of Algebras
Published online by Cambridge University Press: 20 November 2018
Extract
The concept of the universal enveloping algebra 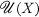 of a (not necessarily associative) algebra X is basic to the study of the representations of X, because there is a one-to-one correspondence between the representations of X and
of a (not necessarily associative) algebra X is basic to the study of the representations of X, because there is a one-to-one correspondence between the representations of X and 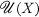 . If one is only interested in studying a certain class of the representations of X, the thought occurs that there may exist a more suitable universal object.
. If one is only interested in studying a certain class of the representations of X, the thought occurs that there may exist a more suitable universal object.
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 1974
References
- 2
- Cited by


