Hostname: page-component-586b7cd67f-gb8f7 Total loading time: 0 Render date: 2024-11-25T07:41:39.759Z Has data issue: false hasContentIssue false
  • English
  • Français

Irreducibility of Bernoulli Polynomials of Higher Order

Published online by Cambridge University Press:  20 November 2018

P. J. McCarthy
P. J. McCarthy*
Affiliation:
University of Kansas
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The Bernoulli polynomials of order k, where k is a positive integer, are defined by

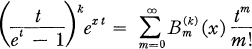
Bm(k)(x) is a polynomial of degree m with rational coefficients, and the constant term of Bm(k)(x) is the mth Bernoulli number of order k, Bm(k). In a previous paper (3) we obtained some conditions, in terms of k and m, which imply that Bm(k)(x) is irreducible (all references to irreducibility will be with respect to the field of rational numbers). In particular, we obtained the following two results.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 14 , 1962 , pp. 565 - 567
Copyright
Copyright © Canadian Mathematical Society 1962

References

1. Carlitz, L., Note on irreducibility of the Bernoulli and Euler polynomials, Duke Math. J., 19 (1952), 475–481.Google Scholar
2. Carlitz, L., A note on Bernoulli numbers of higher order, Scripta Math., 22 (1956), 217–221.Google Scholar
3. McCarthy, P. J., Some irreducibility theorems for Bernoulli polynomials of higher order, Duke Math. J., 27 (1960), 313–318.Google Scholar
4. Nörlund, N. E., Vorlesungen iiber Differenzenrechnung, Berlin (1924).Google Scholar