Article contents
Inversion of the Radon Transform on the Free Nilpotent Lie Group of Step Two
Published online by Cambridge University Press: 20 November 2018
Abstract
Let 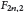 ${{F}_{2n,2}}$ be the free nilpotent Lie group of step two on
${{F}_{2n,2}}$ be the free nilpotent Lie group of step two on 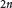 $2n$ generators, and let
$2n$ generators, and let  $\mathbf{P}$ denote the affine automorphism group of
$\mathbf{P}$ denote the affine automorphism group of 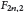 ${{F}_{2n,2}}$. In this article the theory of continuous wavelet transform on
${{F}_{2n,2}}$. In this article the theory of continuous wavelet transform on 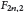 ${{F}_{2n,2}}$ associated with
${{F}_{2n,2}}$ associated with  $\mathbf{P}$ is developed, and then a type of radial wavelet is constructed. Secondly, the Radon transform on
$\mathbf{P}$ is developed, and then a type of radial wavelet is constructed. Secondly, the Radon transform on 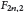 ${{F}_{2n,2}}$ is studied, and two equivalent characterizations of the range for Radon transform are given. Several kinds of inversion Radon transform formulae are established. One is obtained from the Euclidean Fourier transform; the others are from the group Fourier transform. By using wavelet transforms we deduce an inversion formula of the Radon transform, which does not require the smoothness of functions if the wavelet satisfies the differentiability property. In particular, if
${{F}_{2n,2}}$ is studied, and two equivalent characterizations of the range for Radon transform are given. Several kinds of inversion Radon transform formulae are established. One is obtained from the Euclidean Fourier transform; the others are from the group Fourier transform. By using wavelet transforms we deduce an inversion formula of the Radon transform, which does not require the smoothness of functions if the wavelet satisfies the differentiability property. In particular, if 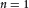 $n\,=\,1$,
$n\,=\,1$, 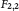 ${{F}_{2,2}}$ is the 3-dimensional Heisenberg group
${{F}_{2,2}}$ is the 3-dimensional Heisenberg group 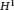 ${{H}^{1}}$, the inversion formula of the Radon transform is valid, which is associated with the sub-Laplacian on
${{H}^{1}}$, the inversion formula of the Radon transform is valid, which is associated with the sub-Laplacian on 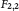 ${{F}_{2,2}}$. This result cannot be extended to the case
${{F}_{2,2}}$. This result cannot be extended to the case 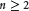 $n\,\ge \,2$.
$n\,\ge \,2$.
Keywords
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 2014
Footnotes
The authors are supported by the National Natural Science Foundation of China (Grant No. 10971039, 11271091).
References
- 1
- Cited by


