Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Breen, Marilyn
1980.
Intersectional properties concerning planarm-convex sets.
Israel Journal of Mathematics,
Vol. 36,
Issue. 1,
p.
83.


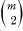 line segments determined by these points lies in
line segments determined by these points lies in 