Hostname: page-component-cd9895bd7-7cvxr Total loading time: 0 Render date: 2024-12-18T15:54:14.540Z Has data issue: false hasContentIssue false
  • English
  • Français

Integral Representation for U3 × GL2

Published online by Cambridge University Press:  20 November 2018

Eric Wambach
Eric Wambach*
Affiliation:
Caltech, Mathematics 253-37, Pasadena, CA 91125, USA email: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Gelbart and Piatetskii-Shapiro constructed various integral representations of Rankin–Selberg type for groups 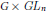$G\,\times \,G{{L}_{n}}$, where 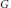$G$ is of split rank $n$. Here we show that their method can equally well be applied to the product 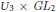${{U}_{3}}\,\times \,G{{L}_{2}}$, where 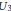${{U}_{3}}$ denotes the quasisplit unitary group in three variables. As an application, we describe which cuspidal automorphic representations of 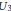${{U}_{3}}$ occur in the Siegel induced residual spectrum of the quasisplit 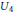${{U}_{4}}$.

Keywords

11F7011F67
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 61 , Issue 6 , 01 December 2009 , pp. 1383 - 1406
Copyright
Copyright © Canadian Mathematical Society 2009

References

[1] Casselman, W. and Shalika, J., The unramified principal series of p-adic groups. II. The Whittaker function. Compositio Math. 41(1980), no. 2, 207–231.Google Scholar
[2] Flicker, Yuval Z., On distinguished representations. J. Reine Angew. Math. 418(1991), 139–172.Google Scholar
[3] Gelbart, S. and Piatetski-Shapiro, I., Automorphic forms and L-functions for the unitary group. In: Lie Group Representations. Lecture Notes in Math. 1041, Springer, Berlin, 1984, pp. 141–184.Google Scholar
[4] Gelbart, S., Piatetski-Shapiro, I., and Rallis, S., Explicit constructions of automorphic L-functions. Lecture Notes in Mathematics 1254, Springer-Verlag, Berlin, 1987.Google Scholar
[5] Gelbart, S., Rogawski, J., and Soudry, D., Endoscopy, theta-liftings, and period integrals for the unitary group in three variables. Ann. of Math. (2) 145(1997), no. 3, 419–476.Google Scholar
[6] Gelbart, Shahidi, Analytic Properties of Automorphic L-functions. Lecture Notes in Mathematics, No. 1254, Springer Verlag, 1987.Google Scholar
[7] Gross, B. H. and Prasad, D., On the decomposition of a representation of SOn when restricted to SOn−1. Canad. J. Math. 44(1992), no. 5, 974–1002.Google Scholar
[8] Harder, G., Langlands, R. P., and Rapoport, M., Algebraische Zyklen auf Hilbert-Blumenthal-Flächen. J. Reine Angew. Math. 366(1986), 53–120.Google Scholar
[9] Jacquet, H., I. I. Piatetskii-Shapiro, and Shalika, J. A., Rankin-Selberg convolutions. Amer. J. Math. 105(1983), no. 2, 367–464.Google Scholar
[10] Jacquet, H. and Shalika, J. A., On Euler products and the classification of automorphic representations. I. Amer. J. Math. 103(1981), no. 3, 499–558.Google Scholar
[11] T., Kon-No, The residual spectrum of U(2, 2). Trans. Amer. Math. Soc. 350(1998), no. 4, 1285–1358.Google Scholar
[12] Koseki, H., and Oda, T., Whittaker functions for the large discrete series representations of SU(2, 1) and related zeta integrals. Publ. Res. Inst. Math. Sci. 31(1995), no. 6, 959–99.Google Scholar
[13] Moeglin, C. and Waldspurger, J.-L., Spectral decomposition and Eisenstein series. Cambridge Tracts in Mathematics 113, Cambridge University Press, Cambridge, 1995. Une paraphrase de l’Écriture [A paraphrase of Scripture].Google Scholar
[14] Rogawski, J. D., Automorphic representations of unitary groups in three variables. Annals of Mathematics Studies 123, Princeton University Press, Princeton, NJ, 1990.Google Scholar
[15] Soudry, D., Rankin–Selberg convolutions for SO2l+1 × GLn : Local Theory. Mem. Amer. Math. Soc. 500(1993).Google Scholar
[16] Soudry, D. On Langlands functoriality from classical groups to GLn. Astérisque 298 (2005), 335–390.Google Scholar
[17] Watanabe, T., A comparison of automorphic L-functions in a theta series lifting for unitary groups. Israel J. Math. 116(2000), 93–116.Google Scholar
[18] S.-W., Zhang, Gross-Zagier formula for GL(2). II. In: Heegner points and Rankin L-series, Math. Sci. Res. Inst. Publ. 49, Cambridge Univ. Press, Cambridge, 2004, pp. 191–214.Google Scholar