Hostname: page-component-cc8bf7c57-qfg88 Total loading time: 0 Render date: 2024-12-11T23:03:20.908Z Has data issue: false hasContentIssue false
  • English
  • Français

Integral Bases in Kummer Extensions of Dedekind Fields

Published online by Cambridge University Press:  20 November 2018

Leon R. McCulloh
Leon R. McCulloh*
Affiliation:
The University of Illinois, Urbana, Illinois
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let J be a Dedekind ring, F its quotient field, F′ a finite separable extension of F, and J′ the integral closure of J in F′. It has been shown by Artin (1) that a necessary and sufficient condition that J′ have an integral basis over J is that a certain ideal of F (namely, √(D/Δ), where D is the discriminant of the extension and Δ is the discriminant of an arbitrary basis of the extension) should be principal. More generally, he showed that if 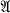is an ideal of F′, then a necessary and sufficient condition that 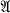have a module basis over J is that N(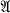)√(D/Δ) should be principal.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 15 , 1963 , pp. 755 - 765
Copyright
Copyright © Canadian Mathematical Society 1963

References

1. Artin, E., Questions de base minimale dans la théorie des nombres algébriques, Algèbre et Théorie des Nombres, Colloques Internationaux du Centre National de la Recherche Scientifique, No. 24, pp. 19–20 (Paris, 1950).Google Scholar
2. Butts, H. S. and Mann, H. B., Corresponding residue systems in algebraic number fields, Pacific J. Math., 6 (1956), 211–224.Google Scholar
3. Hecke, E., Vorlesungen ueber die Théorie der algebraischen Zahlen (New York, 1948).Google Scholar
4. Mann, H. B., Introduction to algebraic number theory (Columbus, 1955).Google Scholar
5. Mann, H. B., On integral bases, Proc. Amer. Math. Soc, 9 (1958), 167–172.Google Scholar