Hostname: page-component-cd9895bd7-gvvz8 Total loading time: 0 Render date: 2024-12-18T15:44:06.853Z Has data issue: false hasContentIssue false
  • English
  • Français

Inequalities for the Surface Area of Projections of Convex Bodies

Published online by Cambridge University Press:  20 November 2018

Apostolos Giannopoulos ,
Alexander Koldobsky  and
Petros Valettas
Apostolos Giannopoulos
Affiliation:
Department of Mathematics, National and Kapodistrian University of Athens, Panepistimioupolis 157-84, Athens, Greece email: [email protected]
Alexander Koldobsky
Affiliation:
Department of Mathematics, University of Missouri, Columbia, MO, USA email: [email protected]@missouri.edu
Petros Valettas
Affiliation:
Department of Mathematics, University of Missouri, Columbia, MO, USA email: [email protected]@missouri.edu
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We provide general inequalities that compare the surface area 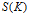$S(K)$ of a convex body 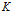$K$ in ${{\mathbb{R}}^{n}}$ to the minimal, average, or maximal surface area of its hyperplane or lower dimensional projections. We discuss the same questions for all the quermassintegrals of 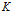$K$. We examine separately the dependence of the constants on the dimension in the case where 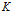$K$ is in some of the classical positions or 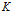$K$ is a projection body. Our results are in the spirit of the hyperplane problem, with sections replaced by projections and volume by surface area.

Keywords

52A2046B05surface areaconvex bodyprojection
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 70 , Issue 4 , 01 August 2018 , pp. 804 - 823
Copyright
Copyright © Canadian Mathematical Society 2018

References

[1] Artstein-Avidan, S., Giannopoulos, A., and Milman, V. D., Asymptotic geometric analysis. Vol. I. Mathematical Surveys and Monographs, 202, American Mathematical Society, Providence, RI, 2015. http://dx.doi.Org/10.1090/surv/202 Google Scholar
[2] Ball, K. M., Volume ratios and a reverse isoperimetric inequality. J. London Math. Soc. (2) 44(1991), no. 2, 351–359. http://dx.doi.Org/10.1112/jlms/s2-44.2.351 Google Scholar
[3] Brazitikos, S., Giannopoulos, A., Valettas, P., and Vritsiou, B.-H., Geometry ofisotropic convex bodies. Mathematical Surveys and Monographs, 196, American Mathematical Society, Providence, RI, 2014. http://dx.doi.Org/10.1090/surv/196 Google Scholar
[4] Burago, Y. D. and Zalgaller, V. A., Geometric inequalities. Springer Series in Soviet Mathematics, Springer-Verlag, Berlin-New York, 1988. http://dx.doi.org/10.1007/978-3-662-07441-1 Google Scholar
[5] Fradelizi, M., Giannopoulos, A., and Meyer, M., Some inequalities about mixed volumes. Israel J. Math. 135(2003), 157–179. http://dx.doi.org/10.1007/BF02776055 Google Scholar
[6] Gardner, R. J., Geometric tomography. Second Ed., Encyclopedia of Mathematics and its Applications, 58, Cambridge University Press, Cambridge, 2006. http://dx.doi.Org/10.1017/CBO9781107341029 Google Scholar
[7] Giannopoulos, A., Hartzoulaki, M., and Paouris, G., On a local version of the Aleksandrov-Fenchel inequality for the quermassintegrals of a convex body. Proc. Amer. Math. Soc. 130(2002), no. 8, 2403–2412. http://dx.doi.org/10.1090/S0002-9939-02-06329-3 Google Scholar
[8] Giannopoulos, A. and Milman, V. D., Extremal problems and isotropic positions of convex bodies. Israel J. Math. 117(2000), 29–60. http://dx.doi.org/10.1007/BF02773562 Google Scholar
[9] Giannopoulos, A. and Papadimitrakis, M., Isotropic surface area measures. Mathematika 46(1999), 1–13. http://dx.doi.org/10.1112/S0025579300007518 Google Scholar
[10] Koldobsky, A., Stability and separation in volume comparison problems. Math. Model. Nat. Phenom. 8(2013), 156–169. http://dx.doi.org/10.1051/mmnp/20138111 Google Scholar
[11] Koldobsky, A., Stability inequalities for projections of convex bodies. Discrete Comput. Geom. 57(2017), 152–163. http://dx.doi.org/10.1007/s00454-016-9844-9 Google Scholar
[12] Markessinis, E., Paouris, G., and Saroglou, Ch., Comparing the M-position with some classical positions of convex bodies. Math. Proc. Cambridge Philos. Soc. 152(2012), 131–152. http://dx.doi.Org/10.1017/S0305004111000703 Google Scholar
[13] Petty, C. M., Surface area of a convex body under affme transformations. Proc. Amer. Math. Soc. 12(1961), 824–828. http://dx.doi.org/10.1090/S0002-9939-1961-0130618-0 Google Scholar
[14] Schneider, R., Convex bodies: The Brunn-Minkowski theory. Second expanded ed., Encyclopedia of Mathematics and its Applications, 151, Cambridge University Press, Cambridge, 2014.Google Scholar
[15] Schneider, R. and Weil, W., Zonoids and selected topics. In: Convexity and its Applications, Birkhauser, Boston, Mass., 1983.Google Scholar