Hostname: page-component-78c5997874-j824f Total loading time: 0 Render date: 2024-11-13T11:31:36.756Z Has data issue: false hasContentIssue false
  • English
  • Français

Induced Coactions of Discrete Groups on C*-Algebras

Published online by Cambridge University Press:  20 November 2018

Siegfried Echterhoff  and
John Quigg
Siegfried Echterhoff
Affiliation:
Westfälishche Wilhelms-Universität Münster, SFB 478, Hittorfstrasse 27, D-48149 Münster, Germany email: [email protected]
John Quigg
Affiliation:
Department of Mathematics, Arizona State University, Tempe, Arizona 85287, U.S.A. email: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Using the close relationship between coactions of discrete groups and Fell bundles, we introduce a procedure for inducing a 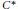${{C}^{*}}$ -coaction 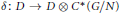$\delta :D\to D\otimes {{C}^{*}}\left( G/N \right)$ of a quotient group 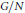$G/N$ of a discrete group 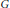$G$ to a 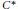${{C}^{*}}$-coaction 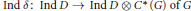$\text{Ind}\,\delta \text{:}\,\text{Ind}\,D\to \text{Ind}\,D\otimes {{C}^{*}}\left( G \right)\,\text{of }G$. We show that induced coactions behave in many respects similarly to induced actions. In particular, as an analogue of the well known imprimitivity theorem for induced actions we prove that the crossed products 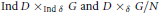$\text{Ind}\,D{{\times }_{\text{Ind}\,\delta }}\,G\,\text{and }D{{\times }_{\delta }}\,G/N$ are always Morita equivalent. We also obtain nonabelian analogues of a theorem of Olesen and Pedersen which show that there is a duality between induced coactions and twisted actions in the sense of Green. We further investigate amenability of Fell bundles corresponding to induced coactions.

Keywords

46L55
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 51 , Issue 4 , 01 August 1999 , pp. 745 - 770
Copyright
Copyright © Canadian Mathematical Society 1999

References

[1] Abadie, B. and Exel, R., Deformation quantization via Fell bundles. Math. Scand, to appear.Google Scholar
[2] Cuntz, J. and Krieger, W., A class of C*-algebras and topologicalMarkov chains. Invent.Math. 56(1980), 251–268.Google Scholar
[3] Echterhoff, S., On induced covariant systems. Proc. Amer.Math. Soc. 108(1990), 703–706.Google Scholar
[4] Echterhoff, S. and Raeburn, I., Induced C*-algebras, coactions, and equivariance in the symmetric imprimitivity theorem. Preprint.Google Scholar
[5] Echterhoff, S. and Raeburn, I., The stabilisation trick for coactions. J. Reine Angew.Math. 470(1996), 181–215.Google Scholar
[6] Exel, R., Circle actions on C*-algebras, partial automorphisms, and a generalized Pimsner-Voiculescu exact sequence. J. Funct. Anal. 122(1994), 361–401.Google Scholar
[7] Exel, R., Amenability for Fell bundles. J. Reine Angew.Math. 492(1997), 41–73.Google Scholar
[8] Fell, J. M. G., Weak containment and induced representations of groups. II. Trans. Amer.Math. Soc. 110(1964), 424–447.Google Scholar
[9] Fell, J. M. G. and Doran, R. S., Representations of *-Algebras, Locally Compact Groups, and Banach * -Algebraic Bundles. Vol. 2, Academic Press, 1988.Google Scholar
[10] Gootman, E. and Lazar, A., Applications of non-commutative duality to crossed product C*-algebras determined by an action or coaction. Proc. LondonMath. Soc. 59(1989), 593–624.Google Scholar
[11] Green, P., The local structure of twisted covariance algebras. Acta Math. 140(1978), 191–250.Google Scholar
[12] Hertz, C., Harmonic synthesis for subgroups. Ann. Inst. Fourier (Grenoble) 23(1973), 91–123.Google Scholar
[13] Imai, S. and Takai, H., On a duality for C*-crossed products by a locally compact group. J. Math. Soc. Japan 30(1978), 495–504.Google Scholar
[14] Katayama, Y., Takesaki's duality for a non-degenerate co-action. Math. Scand. 55(1985), 141–151.Google Scholar
[15] Kumjian, A., Fell bundles over groupoids. Proc. Amer.Math. Soc. 126(1998), 1115–1125.Google Scholar
[16] Landstad, M. B., Duality theory for covariant systems. Trans. Amer.Math. Soc. 248(1979), 223–267.Google Scholar
[17] Landstad, M. B., Phillips, J., Raeburn, I., and Sutherland, C. E., Representations of crossed products by coactions and principal bundles. Trans. Amer.Math. Soc. 299(1987), 747–784.Google Scholar
[18] Nilsen, M., Full crossed products by coactions, C0(X)-algebras and C*-bundles. Preprint, 1996.Google Scholar
[19] Olesen, D. and Pedersen, G. K., Applications of the Connes spectrum to C*-dynamical systems, III. J. Funct. Anal. 45(1982), 357–390.Google Scholar
[20] Olesen, D. and Pedersen, G. K., Partially inner C*-dynamical systems. J. Funct. Anal. 66(1986), 262–281.Google Scholar
[21] Phillips, J. and Raeburn, I., Twisted crossed products by coactions. J. Austral.Math. Soc. Ser. A 56(1994), 320–344.Google Scholar
[22] Quigg, J., Full and reduced C*-coactions. Math. Proc. Cambridge Philos. Soc. 116(1994), 435–450.Google Scholar
[23] Quigg, J., Discrete C*-coactions and C*-algebraic bundles. J. Austral. Math. Soc. Ser. A 60(1996), 204–221.Google Scholar
[24] Quigg, J. and Raeburn, I., Induced C*-algebras and Landstad duality for twisted coactions. Trans. Amer.Math. Soc. 347(1995), 2885–2915.Google Scholar
[25] Quigg, J. and Raeburn, I., Characterizations of crossed products by partial actions. J. Operator Theory 37(1997), 311–340.Google Scholar
[26] Raeburn, I., A duality theorem for crossed products by nonabelian groups. Proc. Cent. Math. Anal. Austral. Nat. Univ. 15(1987), 214–227.Google Scholar
[27] Raeburn, I., Induced C*-algebras and a symmetric imprimitivity theorem. Math. Ann. 280(1988), 369–387.Google Scholar
[28] Rieffel, M. A., Induced representations of C*-algebras. Adv. inMath. 13(1974), 176–257.Google Scholar