Hostname: page-component-586b7cd67f-vdxz6 Total loading time: 0 Render date: 2024-11-24T12:37:11.002Z Has data issue: false hasContentIssue false
  • English
  • Français

Indicator Sets in an Affine Space of any Dimension

Published online by Cambridge University Press:  20 November 2018

F. A. Sherk
F. A. Sherk*
Affiliation:
University of Toronto, Toronto, Ontario
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

It is well known that a translation plane can be represented in a vector space over a field F where F is a subfield of the kernel of a quasifield which coordinatizes the plane [1; 2; 4, p.220; 10]. If II is a finite translation plane of order qr (q = pn, p any prime), then II may be represented in V2r(q), the vector space of dimension 2r over GF(q), as follows:

(i) The points of II are the vectors in V = V2r(q)

(ii) The lines of II are

(a) A set 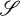of qr + 1 mutually disjoint r-dimensional subspaces of V.

(b) All translates of 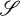in V.

(iii) Incidence is inclusion.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 31 , Issue 1 , 01 February 1979 , pp. 211 - 224
Copyright
Copyright © Canadian Mathematical Society 1979

References

1. André, J., Uber nicht-Desarquessche Ebenen mit transitiver. Translationsgruppe, Math. Zei. 60 (1954), 156–186.Google Scholar
2. Bruck, R. H. and Bose, R. C., The construction of translation planes from projective spaces, J. Algebr. 1 (1964), 85–102.Google Scholar
3. Bruen, A., Spreads and a conjecture of Bruck and Bose, J. Algebr. 23 (1972), 519–537.Google Scholar
4. Dembowski, P., Finite geometries (Springer-Verlag, Berlin, 1968).Google Scholar
5. Foulser, D. A., Collineation groups of generalized André planes, Can. J. Math. 21 (1969), 358–369.Google Scholar
6. Hering, C., Eine nicht-desarquessche zweifach transitive affine Ebene der Ordnung 27, Abh. Math. Sem. Hamb. 34 (1969), 203–208.Google Scholar
7. Lunelburg, H., Die Suzukigruppen und ihre Geometrien (Springer-Verlag, Berlin, 1965).Google Scholar
8. Maduram, D. M., Matrix representation of translation planes, Geometriae Dedicat. 4 (1975), 485–492.Google Scholar
9. Ostrom, T. G., A characterization of generalized André planes, Math. Zeit. 110 (1969), 1–9.Google Scholar
10. Ostrom, T. G., Finite translation planes (Springer-Verlag, Berlin, 1970).Google Scholar
11. Ostrom, T. G., Classification of finite translation planes, Proceedings of the international conference on projective planes held at Washington State University, April 25-28, 1973 (Washington State University Press, 1973).Google Scholar
12. Rao, M. L. N. and Rao, K. K., A new flag transitive affine plane of order 27, Proc. of the Amer. Math. Soc. 59 (1976), 337–345.Google Scholar
13. Sherk, F. A. and Pabst, G., Indicator sets, reguli, and new a class of spreads, Can. J. Math. 29 (1977), 132–154.Google Scholar