Article contents
Incidence Relations in MulticoherentSpaces II
Published online by Cambridge University Press: 20 November 2018
Extract
Introduction. One standard method of studying the incidences of a system of sets A 1, A2, .… , An is to consider the nerve 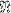 of the system. However, this gives no direct information as to the numbers of components of the various intersections of the sets—information which would be desirable in several geometrical problems. The object of the present paper is to modify the definition of the nerve so that these numbers of components can be taken into account, and to study this modified nerve
of the system. However, this gives no direct information as to the numbers of components of the various intersections of the sets—information which would be desirable in several geometrical problems. The object of the present paper is to modify the definition of the nerve so that these numbers of components can be taken into account, and to study this modified nerve 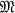 for systems of sets in a connected, locally connected, normal T1 space S of a given degree of multicoherence r(S). The principal result (Theorem 6, 6.4) is a refinement of a theorem of Eilenberg [4, p. 107], and asserts that, if
for systems of sets in a connected, locally connected, normal T1 space S of a given degree of multicoherence r(S). The principal result (Theorem 6, 6.4) is a refinement of a theorem of Eilenberg [4, p. 107], and asserts that, if 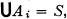 then under suitable hypotheses we have
then under suitable hypotheses we have
(1) 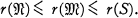
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 1950
References
- 5
- Cited by


