Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Taylor, B. A.
and
Williams, D. L.
1970.
The peak sets of 𝐴^{𝑚}.
Proceedings of the American Mathematical Society,
Vol. 24,
Issue. 3,
p.
604.
Caughran, James G.
1970.
Zeros of analytic functions with infinitely differentiable boundary values.
Proceedings of the American Mathematical Society,
Vol. 24,
Issue. 4,
p.
700.
Alexander, H
Taylor, B.A
and
Williams, D.L
1971.
The interpolating sets for A∞.
Journal of Mathematical Analysis and Applications,
Vol. 36,
Issue. 3,
p.
556.
Taylor, B. A.
and
Williams, D. L.
1972.
Boundary zero sets of 𝐴^{∞} functions satisfying growth conditions.
Proceedings of the American Mathematical Society,
Vol. 35,
Issue. 1,
p.
155.
Korenblyum, B. I.
1973.
Closed ideals in the ring An.
Functional Analysis and Its Applications,
Vol. 6,
Issue. 3,
p.
203.
Chollet, Anne-Marie
1973.
L'Analyse Harmonique dans le Domaine Complexe.
Vol. 336,
Issue. ,
p.
144.
Korolevich, V. S.
and
Pogorelyi, E. A.
1974.
On the zeros of analytic functions belonging to Gevrey classes.
Mathematical Notes of the Academy of Sciences of the USSR,
Vol. 15,
Issue. 6,
p.
514.
Dyn'kin, E. M.
1975.
Growth of an analytic function near its set of singular points.
Journal of Soviet Mathematics,
Vol. 4,
Issue. 4,
p.
438.
Korenblum, Boris
1975.
An extension of the Nevanlinna theory.
Acta Mathematica,
Vol. 135,
Issue. 0,
p.
187.
Nikol'skii, N. K.
1976.
Invariant subspaces in the theory of operators and theory of functions.
Journal of Soviet Mathematics,
Vol. 5,
Issue. 2,
p.
129.
Chollet, Anne-Marie
1976.
Spaces of Analytic Functions.
Vol. 512,
Issue. ,
p.
17.
Korenblum, Boris
1977.
A Beurling-type theorem.
Acta Mathematica,
Vol. 138,
Issue. 0,
p.
265.
Osadchii, N. M.
1977.
Approximative units in some Banach algebras of analytical functions.
Ukrainian Mathematical Journal,
Vol. 28,
Issue. 3,
p.
318.
Matheson, A. L.
1977.
Banach Spaces of Analytic Functions.
Vol. 604,
Issue. ,
p.
67.
Renteln, M.
1978.
Topologische Nullteiler und endlich erzeugte Ideale in gewissen Algebren holomorpher Funktionen.
Acta Mathematica Academiae Scientiarum Hungaricae,
Vol. 32,
Issue. 3-4,
p.
229.
Novinger, W. P.
and
Oberlin, D. M.
1978.
Peak sets for Lipschitz functions.
Proceedings of the American Mathematical Society,
Vol. 68,
Issue. 1,
p.
37.
Shapiro, Joel H.
1980.
Hausdorff measure and Carleson thin sets.
Proceedings of the American Mathematical Society,
Vol. 79,
Issue. 1,
p.
67.
Chollet, Anne-Marie
1980.
Complex Approximation.
Vol. 4,
Issue. ,
p.
57.
Atzmon, Aharon
1980.
Operators which are annihilated by analytic functions and invariant subspaces.
Acta Mathematica,
Vol. 144,
Issue. 0,
p.
27.
Khrushchev, S. V.
1981.
Every ideal of the ring C A n is principalis principal.
Journal of Soviet Mathematics,
Vol. 16,
Issue. 3,
p.
1150.
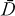 . If f and its first m derivatives belong to A, then the boundary function f(eiθ) belongs to Cm(∂D). The space Am of all such functions is a Banach algebra with the topology induced by Cm(∂D). If all the derivatives of/ belong to A, then the boundary function belongs to C∞(∂D), and the space A∞ all such functions is a topological algebra with the topology induced by C∞(∂D). In this paper we determine the structure of the closed ideals of A∞ (Theorem 5.3).
. If f and its first m derivatives belong to A, then the boundary function f(eiθ) belongs to Cm(∂D). The space Am of all such functions is a Banach algebra with the topology induced by Cm(∂D). If all the derivatives of/ belong to A, then the boundary function belongs to C∞(∂D), and the space A∞ all such functions is a topological algebra with the topology induced by C∞(∂D). In this paper we determine the structure of the closed ideals of A∞ (Theorem 5.3).

