Hostname: page-component-586b7cd67f-r5fsc Total loading time: 0 Render date: 2024-11-27T17:17:01.206Z Has data issue: false hasContentIssue false
  • English
  • Français

Ideal Uniform Polyhedra in 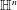$\mathbb{H}^{n}$ and Covolumes of Higher Dimensional Modular Groups

Part of: Zeta and $L$-functions: analytic theory Special aspects of infinite or finite groups Real and complex geometry Linear algebraic groups and related topics Discontinuous groups and automorphic forms

Published online by Cambridge University Press:  27 January 2020

Ruth Kellerhals
Ruth Kellerhals*
Affiliation:
Department of Mathematics, University of Fribourg, CH-1700 Fribourg, Switzerland Email: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Higher dimensional analogues of the modular group 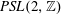$\mathit{PSL}(2,\mathbb{Z})$ are closely related to hyperbolic reflection groups and Coxeter polyhedra with big symmetry groups. In this context, we develop a theory and dissection properties of ideal hyperbolic 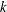$k$-rectified regular polyhedra, which is of independent interest. As an application, we can identify the covolumes of the quaternionic modular groups with certain explicit rational multiples of the Riemann zeta value 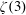$\unicode[STIX]{x1D701}(3)$.

Keywords

Ideal hyperbolic polyhedronk-rectificationNapier cycleCoxeter groupquaternionic modular grouphyperbolic volumezeta value

MSC classification

Primary: 51M10: Hyperbolic and elliptic geometries (general) and generalizations 20F55: Reflection and Coxeter groups 51M25: Length, area and volume
Secondary: 11F06: Structure of modular groups and generalizations; arithmetic groups 20G20: Linear algebraic groups over the reals, the complexes, the quaternions 11M06: $zeta (s)$ and $L(s, chi)$
Type
Article
Information
Canadian Journal of Mathematics , Volume 73 , Issue 2 , April 2021 , pp. 465 - 492
Check for updates
Copyright
© Canadian Mathematical Society 2020

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Ahlfors, L., Möbius transformations in Rn expressed through 2 × 2 matrices of Clifford numbers. Complex Variables Theory Appl. 5(1986), 215–224. https://doi.org/10.1080/17476938608814142CrossRefGoogle Scholar
Ahlfors, L., Möbius transformations and Clifford numbers. In: Differential geometry and complex analysis. Springer, Berlin, 1985, pp. 65–73.CrossRefGoogle Scholar
Coxeter, H., Regular polytopes. Dover Publications Inc., New York, 1973.Google Scholar
Debrunner, H., Dissecting orthoschemes into orthoschemes. Geom. Dedicata 33(1990), 123–152. https://doi.org/10.1007/BF00183080CrossRefGoogle Scholar
Emery, V., On volumes of quasi-arithmetic hyperbolic lattices. Selecta Math. (N.S.) 23(2017), 2849–2862. https://doi.org/10.1007/s00029-017-0308-8CrossRefGoogle Scholar
Grunewald, F. and Kühnlein, S., On the proof of Humbert’s volume formula. Manuscripta Math. 95(1998), 431–436. https://doi.org/10.1007/s002290050039Google Scholar
Guglielmetti, R., Jacquemet, M., and Kellerhals, R., On commensurable hyperbolic Coxeter groups. Geom. Dedicata 183(2016), 143–167. https://doi.org/10.1007/s10711-016-0151-7CrossRefGoogle Scholar
Humphreys, J., Reflection groups and Coxeter groups. Cambridge Studies in Advanced Mathematics, 29, Cambridge University Press, Cambridge, 1990. https://doi.org/10.1017/CBO9780511623646CrossRefGoogle Scholar
Im Hof, H.-C., Napier cycles and hyperbolic Coxeter groups. Bull. Soc. Math. Belg. Sér. A 42(1990), 523–545.Google Scholar
Johnson, N., Integers. Math. Intelligencer 35(2013), 52–59. https://doi.org/10.1007/s00283-012-9357-1CrossRefGoogle Scholar
Johnson, N., Geometries and transformations. Cambridge University Press, Cambridge, 2018. https://doi.org/10.1007/BF01238563CrossRefGoogle Scholar
Johnson, N., Kellerhals, R., Ratcliffe, J., and Tschantz, S., The size of a hyperbolic Coxeter simplex. Transform. Groups 4(1999), 329–353. https://doi.org/10.1007/BF01238563CrossRefGoogle Scholar
Johnson, N. and Weiss, A., Quaternionic modular groups. Linear Algebra Appl. 295(1999), 159–189. https://doi.org/10.1016/S0024-3795(99)00107-XCrossRefGoogle Scholar
Kellerhals, R., On the volume of hyperbolic polyhedra. Math. Ann. 285(1989), 541–569. https://doi.org/10.1007/BF01452047CrossRefGoogle Scholar
Kellerhals, R., On Schläfli’s reduction formula. Math. Z. 206(1991), 193–210. https://doi.org/10.1007/BF02571335CrossRefGoogle Scholar
Kellerhals, R., On the volumes of hyperbolic 5-orthoschemes and the trilogarithm. Comment. Math. Helv. 67(1992), 648–663. https://doi.org/10.1007/BF02566523CrossRefGoogle Scholar
Kellerhals, R., Regular simplices and lower volume bounds for hyperbolic n-manifolds. Ann. Global Anal. Geom. 13(1995), 377–392. https://doi.org/10.1007/BF00773406CrossRefGoogle Scholar
Kellerhals, R., Volumes in hyperbolic 5-space. Geom. Funct. Anal. 5(1995), 640–667. https://doi.org/10.1007/BF01902056CrossRefGoogle Scholar
Kellerhals, R., Collars in PSL (2, H). Ann. Acad. Sci. Fenn. Math. 26(2001), 51–72.Google Scholar
Kellerhals, R., Quaternions and some global properties of hyperbolic 5-manifolds. Canad. J. Math. 55(2003), 1080–1099. https://doi.org/10.4153/CJM-2003-042-4CrossRefGoogle Scholar
Maclachlan, C., Waterman, P., and Wielenberg, N., Higher-dimensional analogues of the modular and Picard groups. Trans. Amer. Math. Soc. 312(1989), 739–753. https://doi.org/10.2307/2001009Google Scholar
Milnor, J., Hyperbolic geometry: the first 150 years. Bull. Amer. Math. Soc. (N.S.) 6(1982), 9–24. https://doi.org/10.1090/S0273-0979-1982-14958-8CrossRefGoogle Scholar
Ratcliffe, J., Foundations of hyperbolic manifolds. Graduate Texts in Mathematics, 149, Springer-Verlag, New York, 1994. https://doi.org/10.1007/978-1-4757-4013-4CrossRefGoogle Scholar
Ratcliffe, J. and Tschantz, S., On volumes of hyperbolic Coxeter polytopes and quadratic forms. Geom. Dedicata 163(2013), 285–299.CrossRefGoogle Scholar
Schläfli, L., Gesammelte mathematische Abhandlungen. Band I, Verlag Birkhäuser, Basel, 1950.CrossRefGoogle Scholar
Vinberg, È., Hyperbolic reflections groups. Uspekhi Mat. Nauk 40(1985), 29–66. 255.Google Scholar
Vinberg, È. and Shvartsman, O., Discrete groups of motions of spaces of constant curvature. Geometry, II, Encyclopaedia Math. Sci., 29, Springer, Berlin, 1993, pp. 139–248. https://doi.org/10.1007/978-3-662-02901-5_2Google Scholar
Wilker, J., The quaternion formalism for Möbius groups in four or fewer dimensions. Linear Algebra Appl. 190(1993), 99–136. https://doi.org/10.1016/0024-3795(93)90222-ACrossRefGoogle Scholar