Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Assouad, Patrice
1984.
Sur les Inégalités Valides dans L1.
European Journal of Combinatorics,
Vol. 5,
Issue. 2,
p.
99.
Witsenhausen, H.S
1986.
Minimum dimension embedding of finite metric spaces.
Journal of Combinatorial Theory, Series A,
Vol. 42,
Issue. 2,
p.
184.
Terwilliger, Paul
and
Deza, Michel
1987.
The classification of finite connected hypermetric spaces.
Graphs and Combinatorics,
Vol. 3,
Issue. 1,
p.
293.
Deza, M.
and
Singhi, N. M.
1988.
Rigid pentagons in hypercubes.
Graphs and Combinatorics,
Vol. 4,
Issue. 1,
p.
31.
Avis, David
and
Mutt
1989.
All the Facets of the Six-point Hamming Cone.
European Journal of Combinatorics,
Vol. 10,
Issue. 4,
p.
309.
Deza, M.
and
Maehara, H.
1990.
Metric transforms and Euclidean embeddings.
Transactions of the American Mathematical Society,
Vol. 317,
Issue. 2,
p.
661.
Wilkeit, Elke
1990.
Isometric embeddings in Hamming graphs.
Journal of Combinatorial Theory, Series B,
Vol. 50,
Issue. 2,
p.
179.
Avis, David
and
Deza, Michel
1991.
The cut cone, L1 embeddability, complexity, and multicommodity flows.
Networks,
Vol. 21,
Issue. 6,
p.
595.
Weichsel, Paul M.
1992.
Distance regular subgraphs of a cube.
Discrete Mathematics,
Vol. 109,
Issue. 1-3,
p.
297.
Bandelt, Hans-Jürgen
and
Dress, Andreas W.M
1992.
A canonical decomposition theory for metrics on a finite set.
Advances in Mathematics,
Vol. 92,
Issue. 1,
p.
47.
Fontana, Walter
Konings, Danielle A. M.
Stadler, Peter F.
and
Schuster, Peter
1993.
Statistics of RNA secondary structures.
Biopolymers,
Vol. 33,
Issue. 9,
p.
1389.
Fukuda, Komei
and
Handa, Keiichi
1993.
Antipodal graphs and oriented matroids.
Discrete Mathematics,
Vol. 111,
Issue. 1-3,
p.
245.
Benayade, Mohammed
and
Fichet, Bernard
1994.
New Approaches in Classification and Data Analysis.
p.
75.
Deza, Michel
and
Laurent, Monique
1994.
Applications of cut polyhedra — I.
Journal of Computational and Applied Mathematics,
Vol. 55,
Issue. 2,
p.
191.
Avis, David
and
Maehara, Hiroshi
1994.
Metric extensions and the L1 hierarchy.
Discrete Mathematics,
Vol. 131,
Issue. 1-3,
p.
17.
Critchley, Frank
and
Fichet, Bernard
1994.
Classification and Dissimilarity Analysis.
Vol. 93,
Issue. ,
p.
5.
De Simone, Caterina
Deza, Michel
and
Laurent, Monique
1994.
Collapsing and lifting for the cut cone.
Discrete Mathematics,
Vol. 127,
Issue. 1-3,
p.
105.
Deza, Antoine
Deza, Michel
and
Grishukhin, Viatcheslav
1998.
Fullerenes and coordination polyhedra versus half-cube embeddings.
Discrete Mathematics,
Vol. 192,
Issue. 1-3,
p.
41.
Klavzar, Sandi
and
Mulder, Henry Martyn
2002.
Partial Cubes and Crossing Graphs.
SIAM Journal on Discrete Mathematics,
Vol. 15,
Issue. 2,
p.
235.
Gravier, Sylvain
Klavžar, Sandi
and
Mollard, Michel
2003.
Isometric embeddings of subdivided wheels in hypercubes.
Discrete Mathematics,
Vol. 269,
Issue. 1-3,
p.
287.
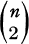 distances between n points. Such a vector d is called a metric if it satisfies the triangle inequalities
distances between n points. Such a vector d is called a metric if it satisfies the triangle inequalities