Article contents
The Hopf Ring for P(n)
Published online by Cambridge University Press: 20 November 2018
Abstract
We show that 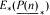 , the E-homology of the Ω-spectrum for P(n), is an E* free Hopf ring for E a complex oriented theory with In sent to 0. This covers the cases
, the E-homology of the Ω-spectrum for P(n), is an E* free Hopf ring for E a complex oriented theory with In sent to 0. This covers the cases 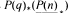 and
and 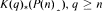 . The generators of the Hopf ring are those necessary for the stable result. The motivation for this paper is to show that P(n) satisfies all of the conditions for the machinery of unstable cohomology operations set up in [BJW95]. This can then be used to produce splittings analogous to those for BP done in [Wil75]
. The generators of the Hopf ring are those necessary for the stable result. The motivation for this paper is to show that P(n) satisfies all of the conditions for the machinery of unstable cohomology operations set up in [BJW95]. This can then be used to produce splittings analogous to those for BP done in [Wil75]
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 1996
References
- 3
- Cited by


